编译原理(双语) 期末复习
注意:部分资料来自 chouxianyu.github.io,版权归原作者所有。
本文图片较多,加载速度受图床服务器网络状况限制,请耐心等待。
概论
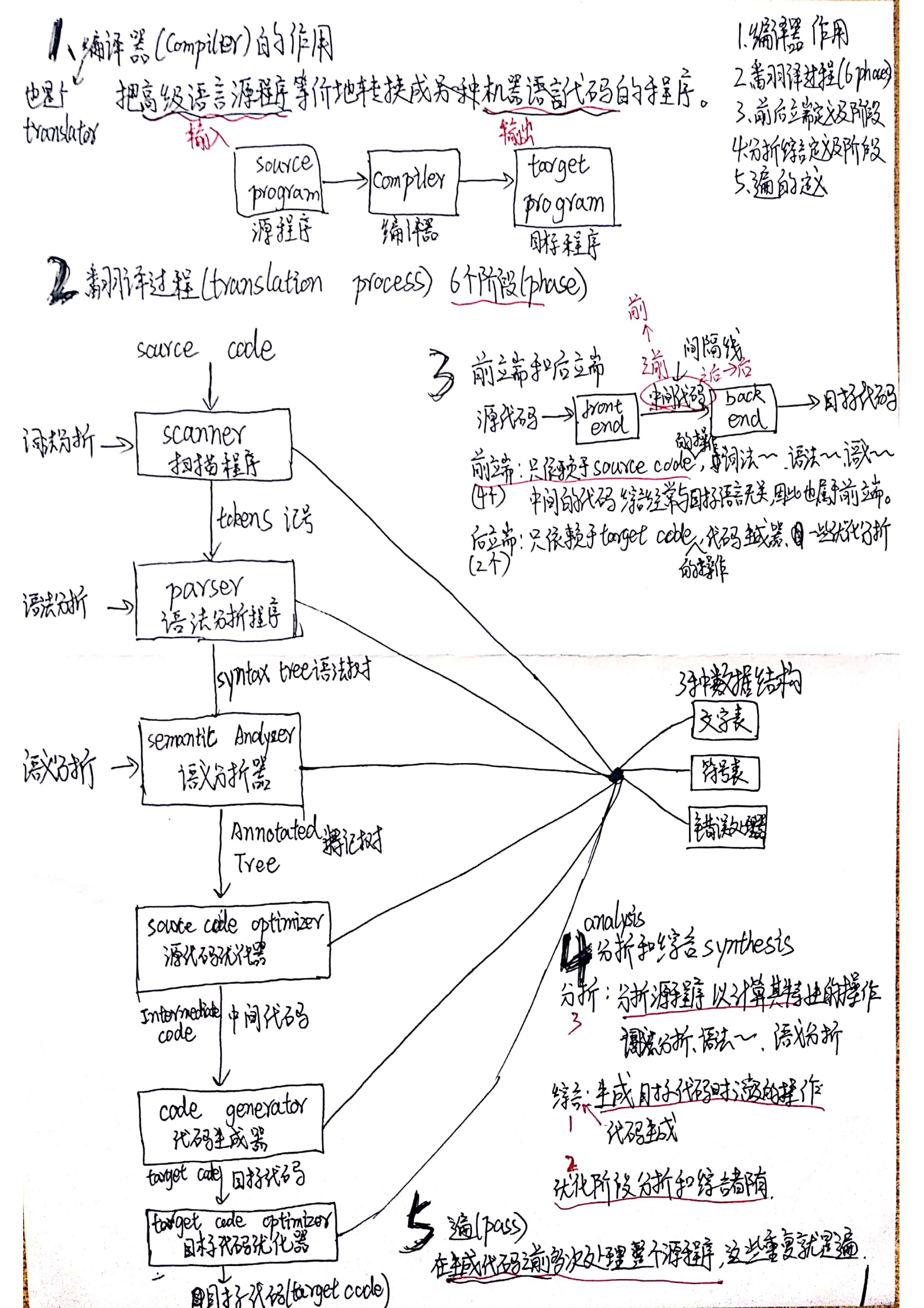
词法分析
lexical analysis 又称为 scanning
正则表达式
regular expressions
概念


题:解释正则式

题:检查匹配

有限自动机
finite automata
DFA

NFA

正则表达式到NFA
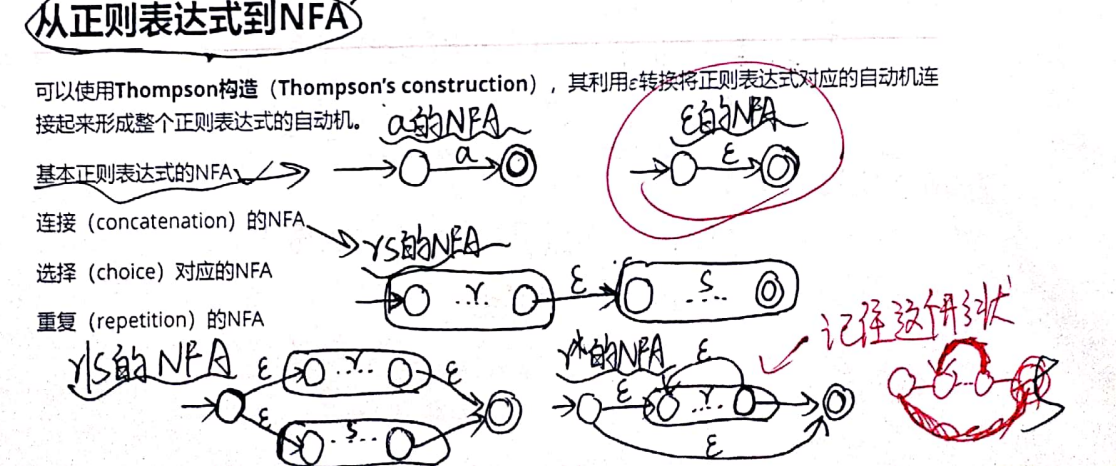
NFA到DFA

最小化DFA

题:正则->NFA->DFA

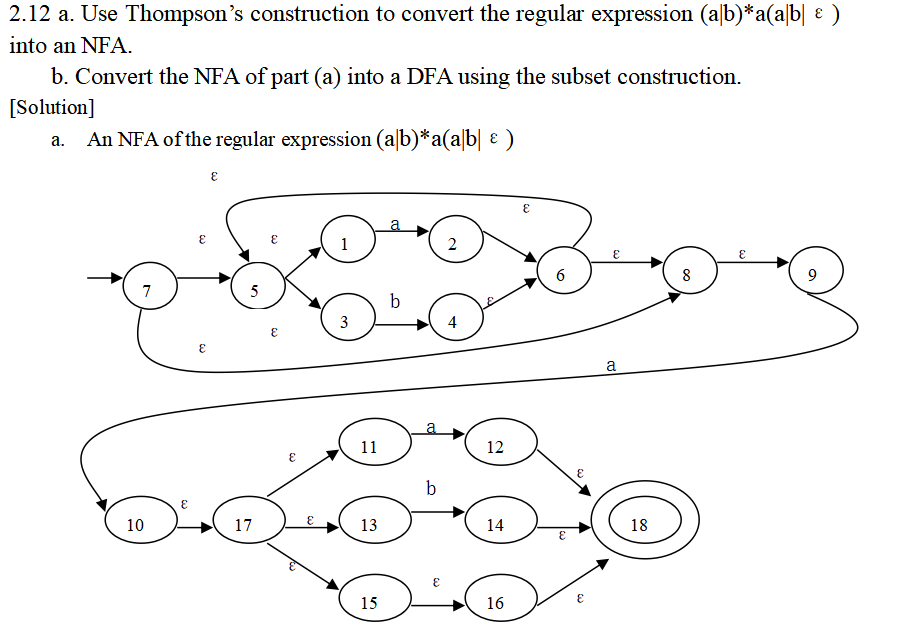
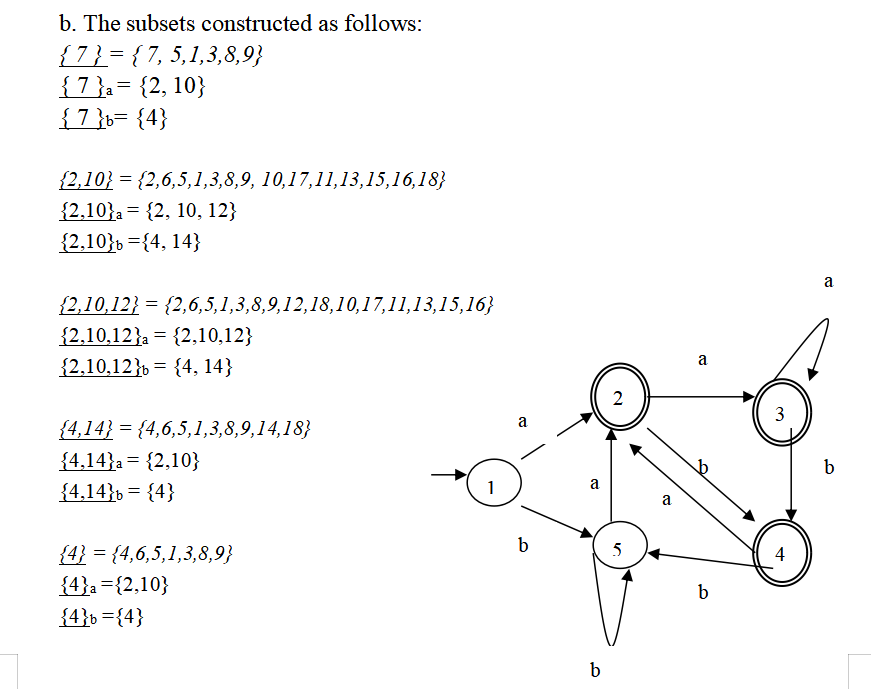
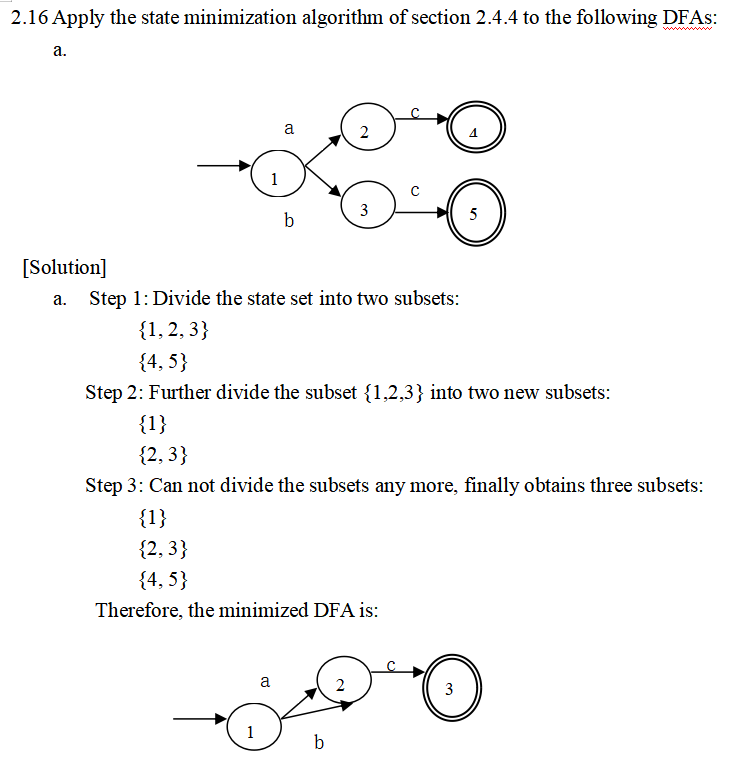
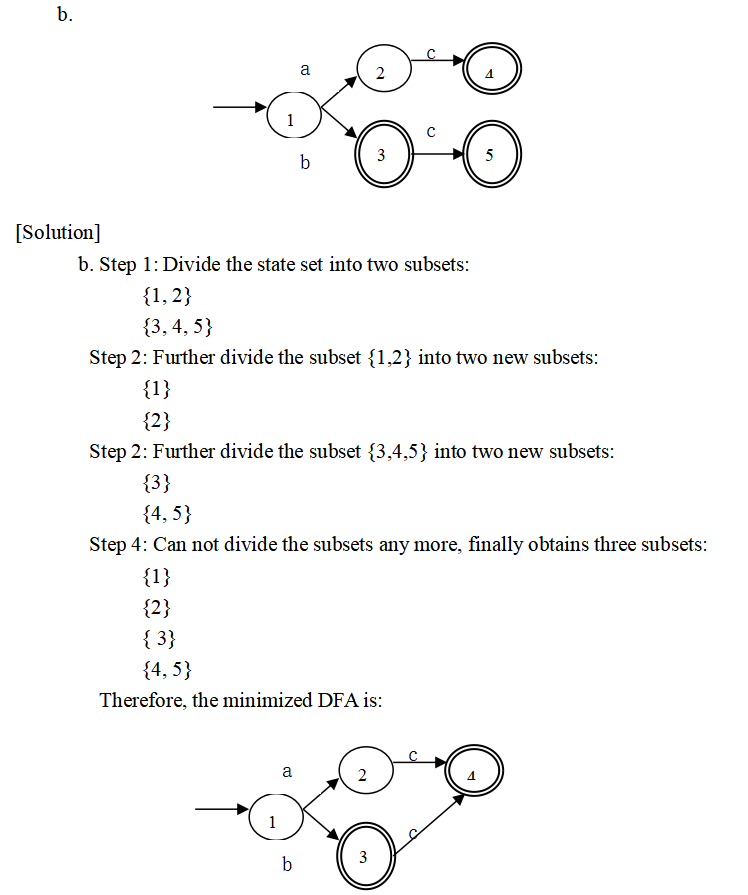
题:最小化DFA
语法分析
上下文无关文法
概念

最左推导 最右推导

分析树

题:列出文法信息

题:最左推导、最右推导

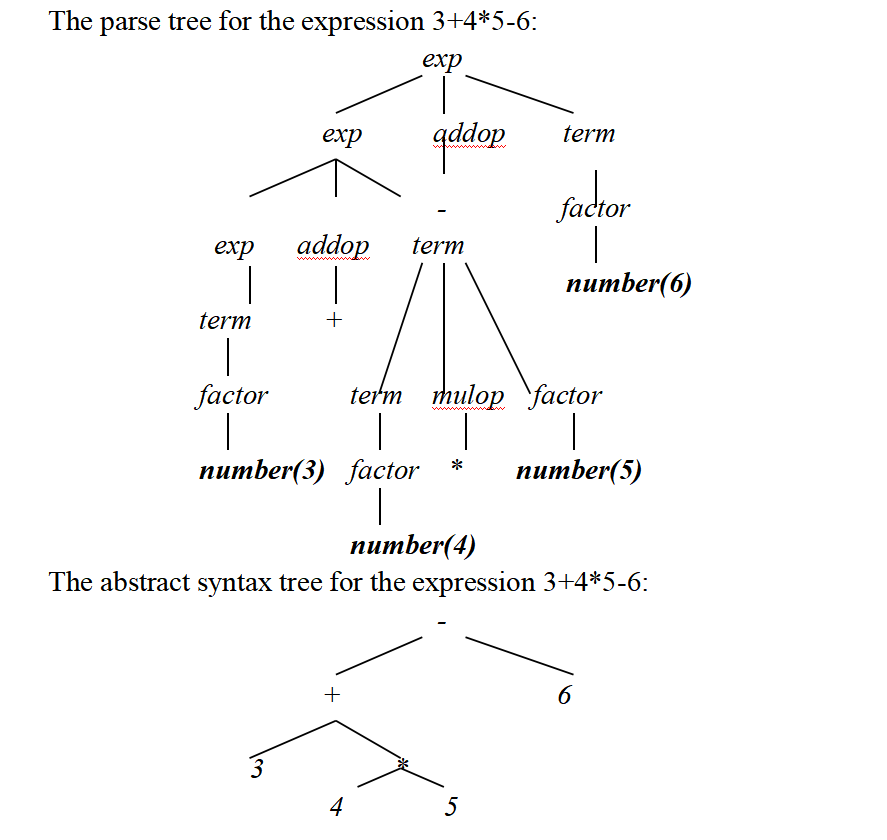
题:分析树、抽象语法树

自底向下分析
LL(1)文法
First集
First集是指对于给定的文法符号,它可能推导出的第一个终结符的集合。
对于一个非终结符A,First(A)表示A能够推导出的所有可能的第一个终结符的集合。
对于一个产生式,First集也可以用于表示该产生式右侧推导出的所有可能的第一个终结符的集合。
First(E) 找E变成的产生式的第一个非终结符的集合

Follow集
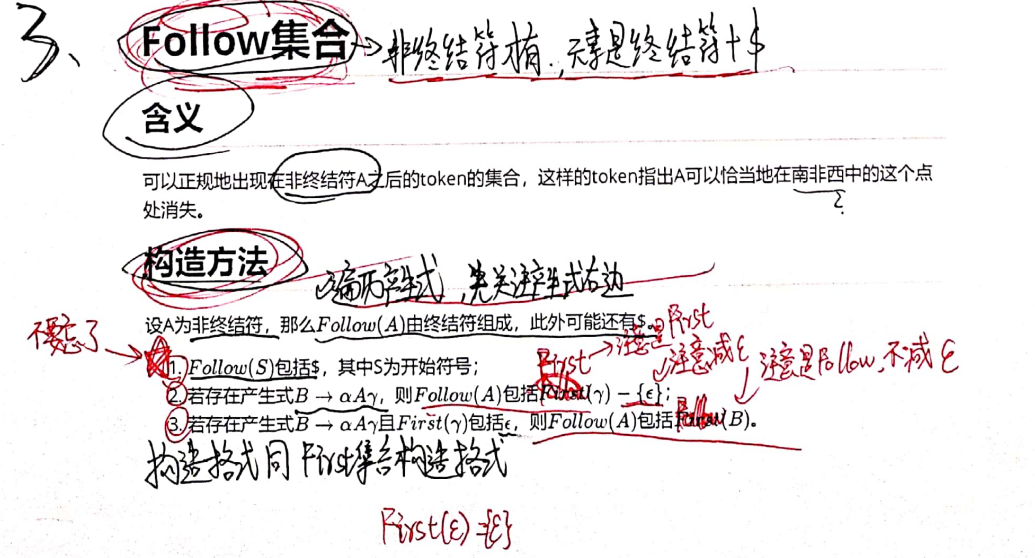
Follow集是指对于给定的非终结符,它在句子中可能紧跟在其后的终结符的集合。对于一个非终结符A,Follow(A)表示在任何一个句子中,A后面可能出现的终结符的集合。
Follow(E) 找E后面可能跟哪些非终结符,如果E在产生式的最后,那么找这个式子的左部后面可能跟哪些非终结符。Follow集里不可能有ε。注意$符号(或#号)

Select集
Select集是用于确定某个产生式是否应该被应用的条件。对于一个产生式P,Select(P)表示当满足某些条件时,产生式P应该被应用。Select集可以通过First集和Follow集计算得出。Select集合里不可能有ε。
对于一个产生式 E -> α,Select(E -> α) = First(α) = First(产生式右部)
如果α可以为ε,Select(E -> α) = First(α) - ε + Follow(E) = First(产生式右部) - ε + Follow(产生式左部)

判定定理

消除左递归


提取左公因子

二义性

文法的二义性是指一个句子在该文法下有两个或多个不同的推导树。消除文法的二义性对于语法分析过程非常重要,因为它可以确保句子具有唯一的语法结构,从而避免歧义。以下是一些常用的方法来消除文法的二义性:
- 重新定义文法规则:
尝试通过重新定义文法规则来消除二义性。这可以包括合并某些规则、拆分规则、重新排列规则等。目标是确保每个句子在新文法下只有一个唯一的推导树。 - 引入优先级和结合性:
为文法中的运算符定义优先级和结合性规则。优先级规则确定了哪些运算符应该优先计算,而结合性规则确定了具有相同优先级的运算符的计算顺序。通过为文法中的运算符分配优先级和结合性,可以消除由于运算符顺序不明确导致的二义性。 - 采用左递归或右递归:
根据需要,可以将文法规则改写为左递归或右递归的形式。左递归适用于左结合的运算符,而右递归适用于右结合的运算符。通过将文法规则改写为适当的递归形式,可以消除由于运算符结合性不明确导致的二义性。
分析表
可以在Select集合的基础上构建,也可以直接构建

分析过程
注意,替换时要反着压入parsing stack
反着压才可以利用select集的定义,让新串与input匹配

题:LL(1)分析表

题:LL(1)分析过程

自底向上分析
LR(0)文法
构造分析表
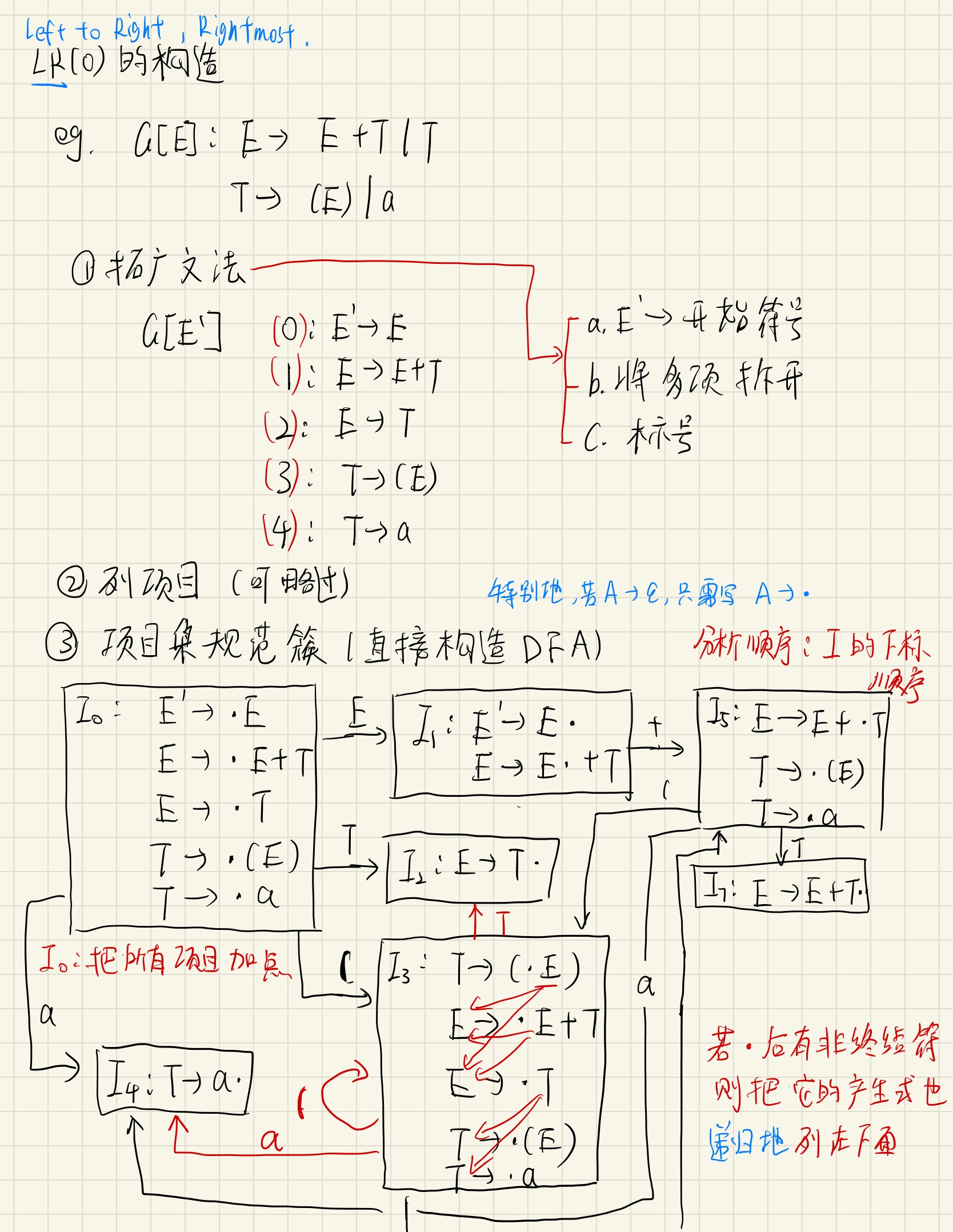
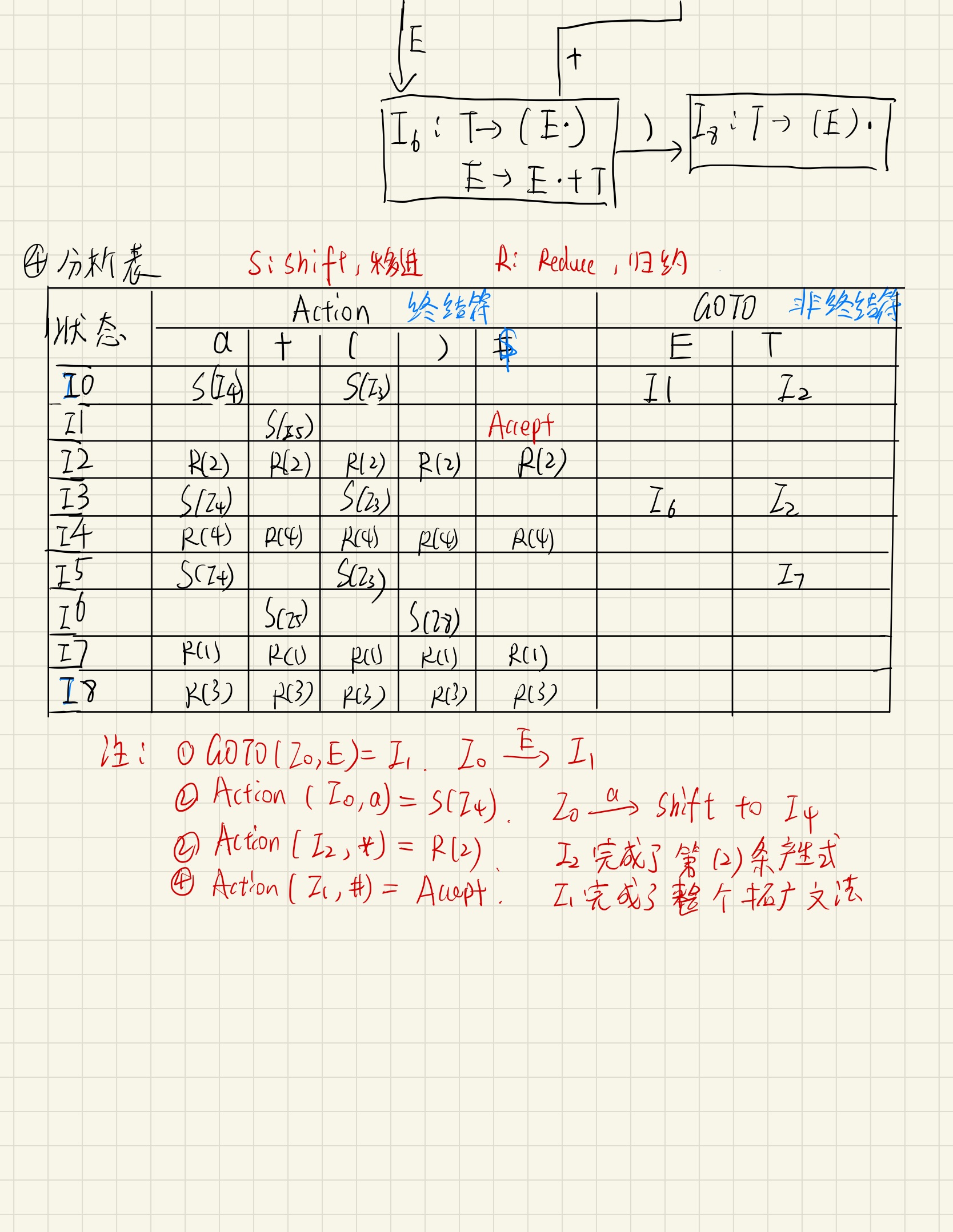
SLR(1)文法
构造分析表

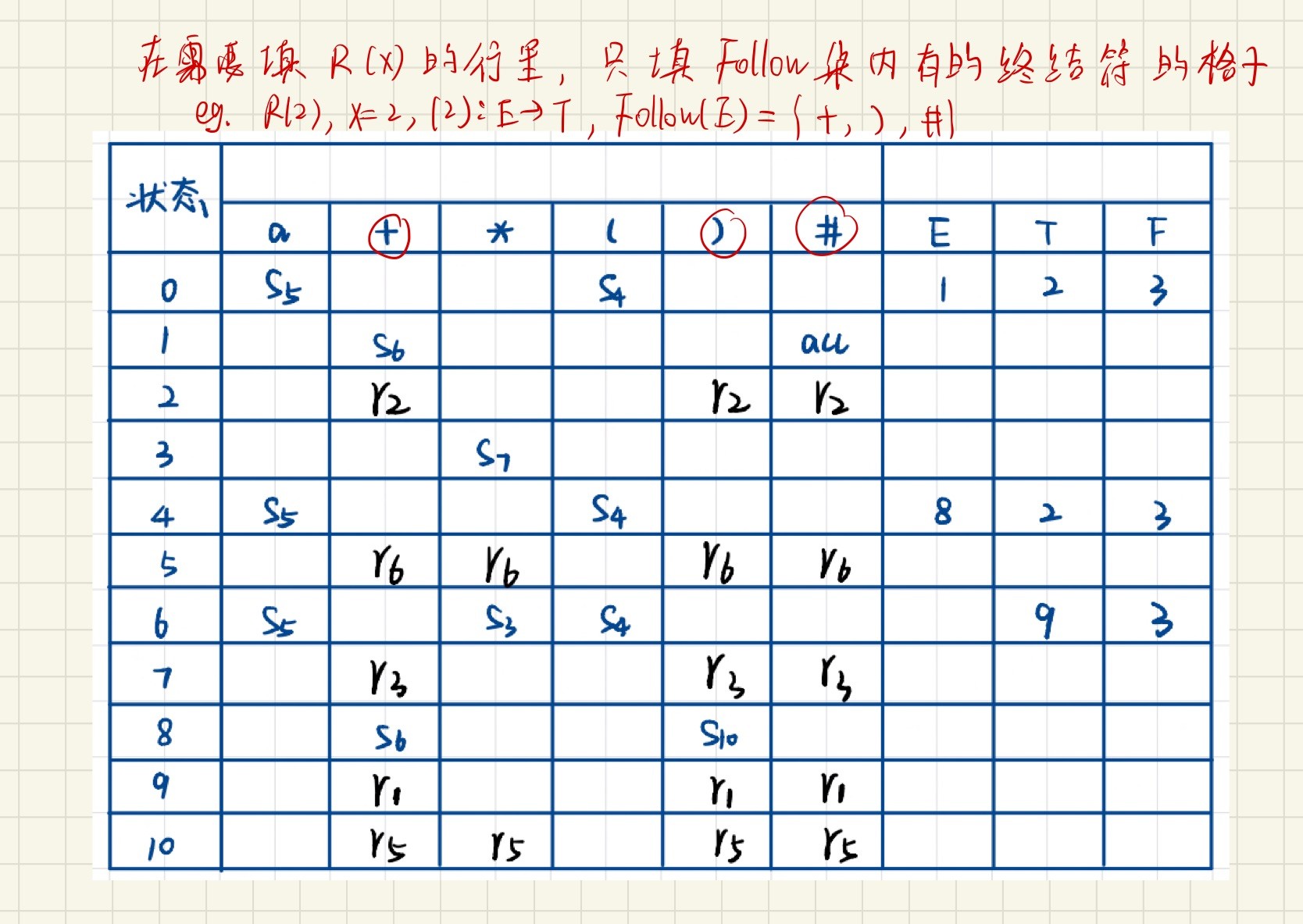
题:SRL(1)文法综合

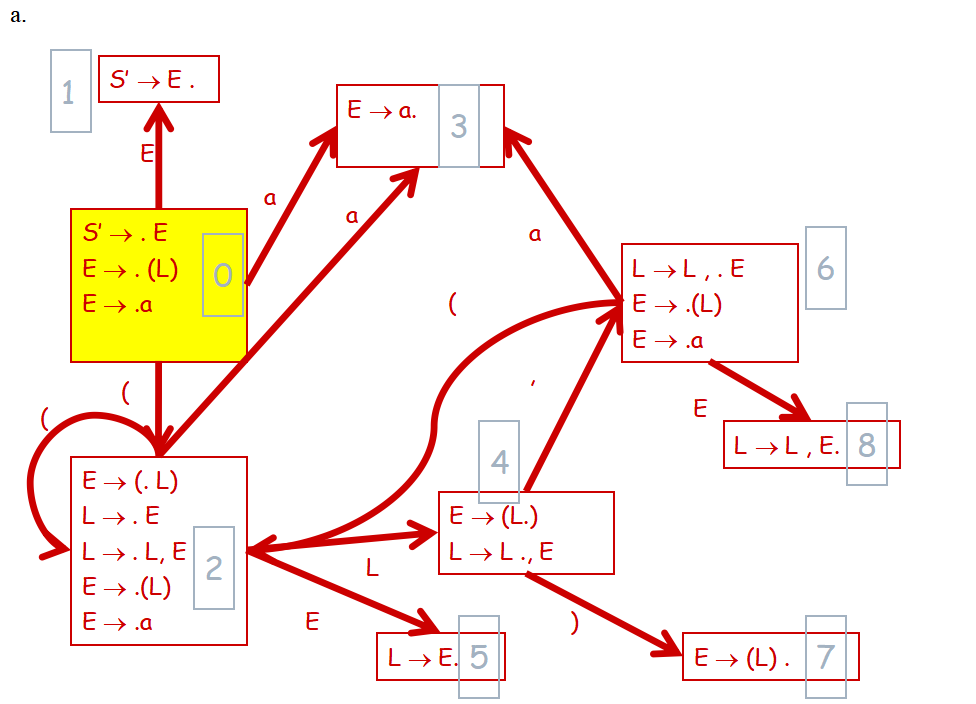

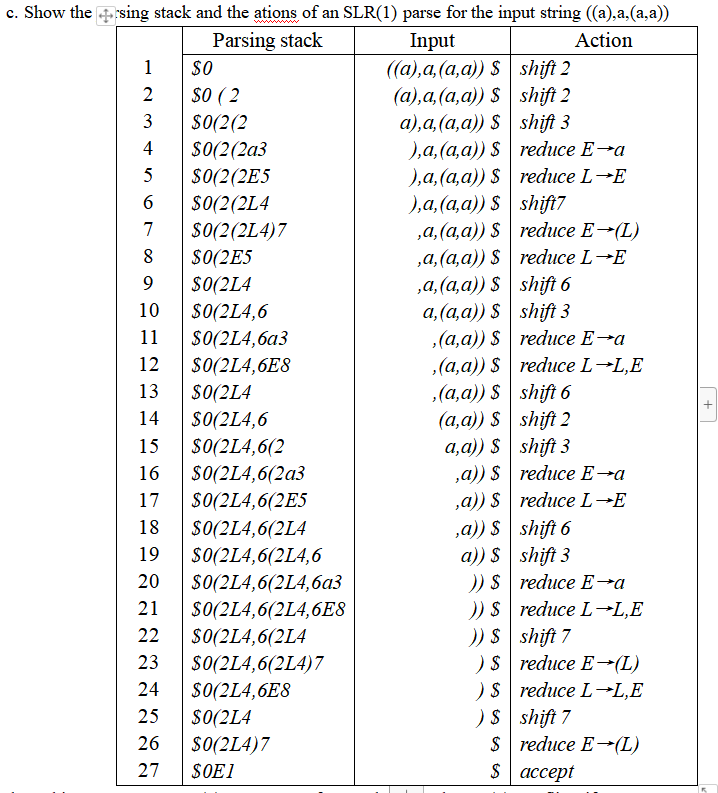

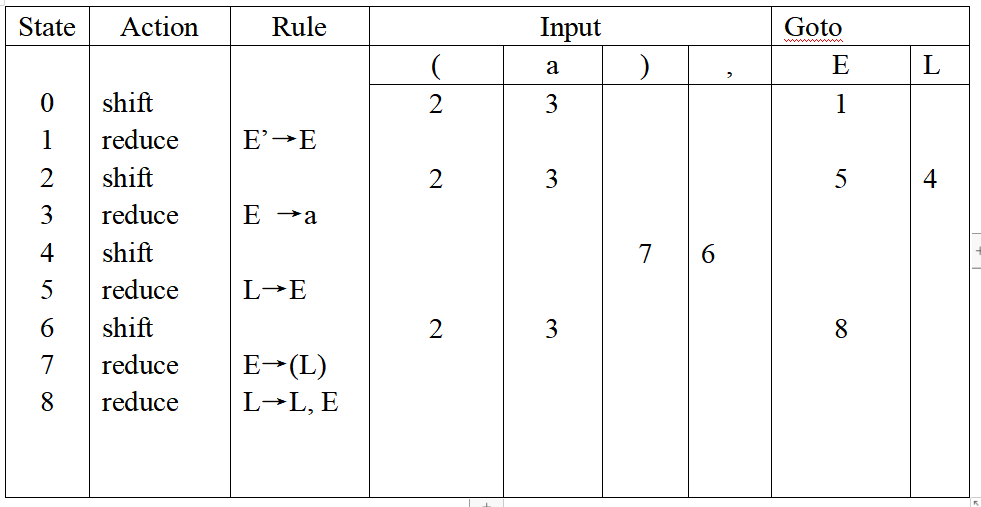
LR(1)文法
构造分析表

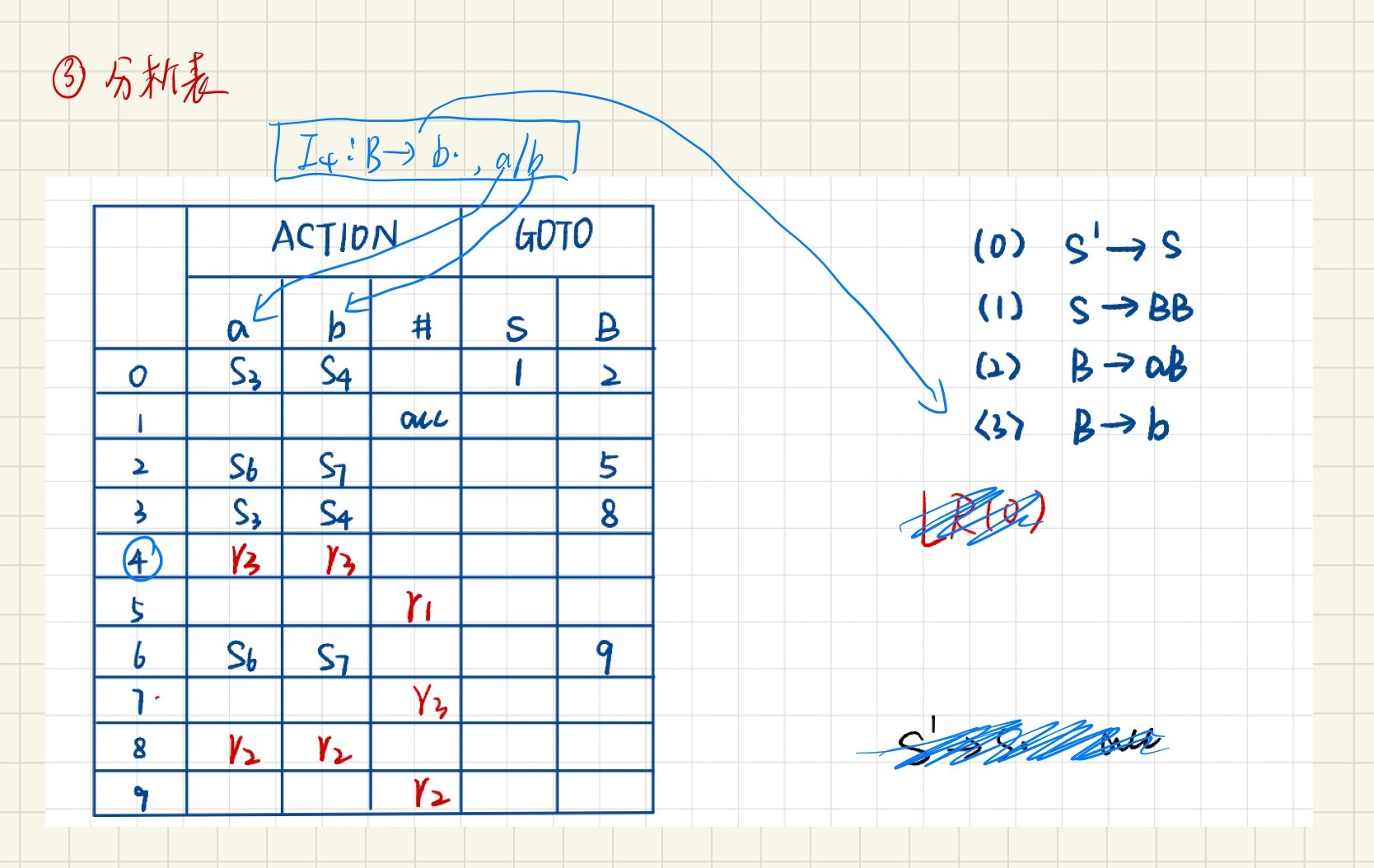
LALR(1)文法
构造分析表
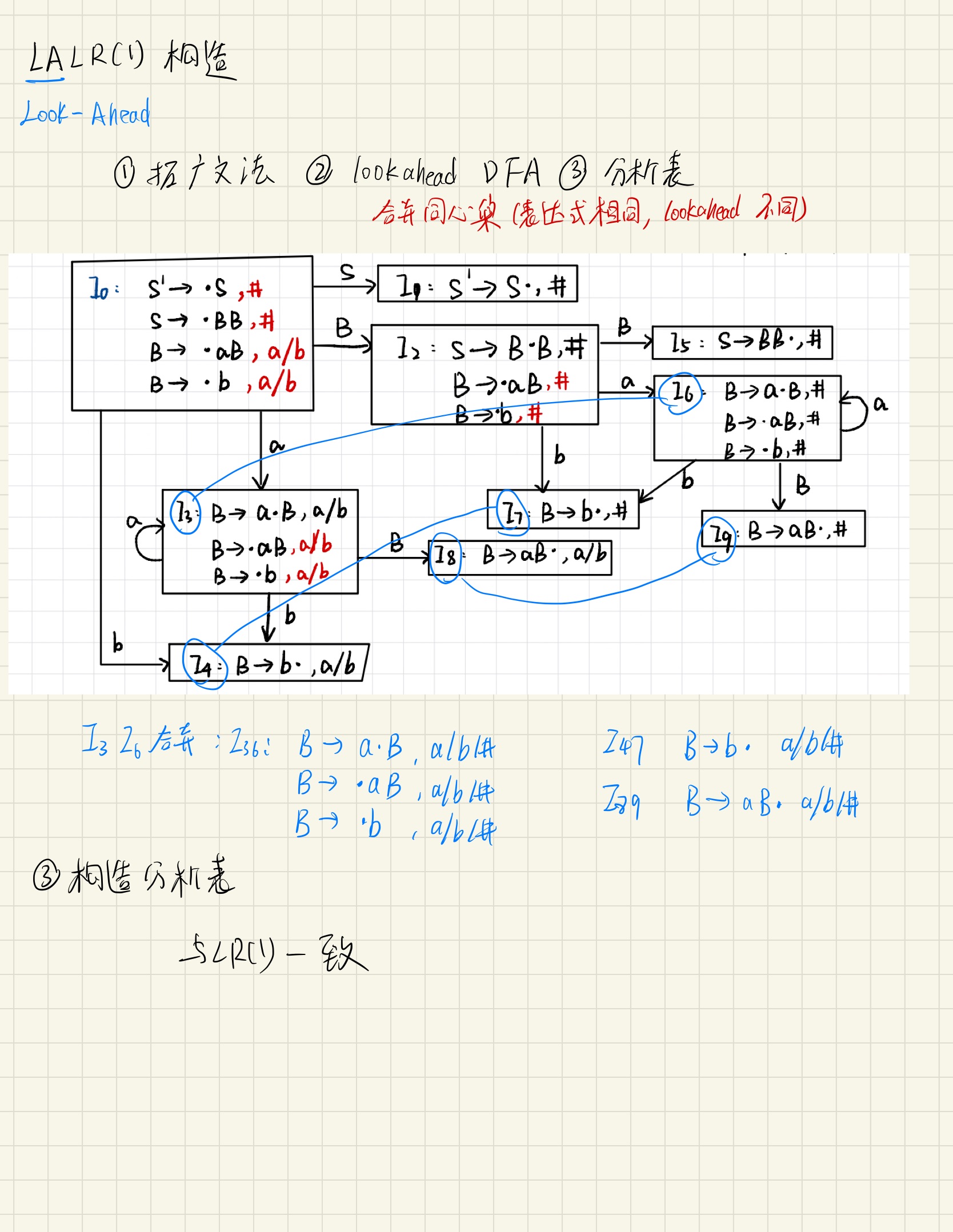
题:LALR(1)文法综合
注:a, b小题是LR(1), c, d小题是LALR(1)


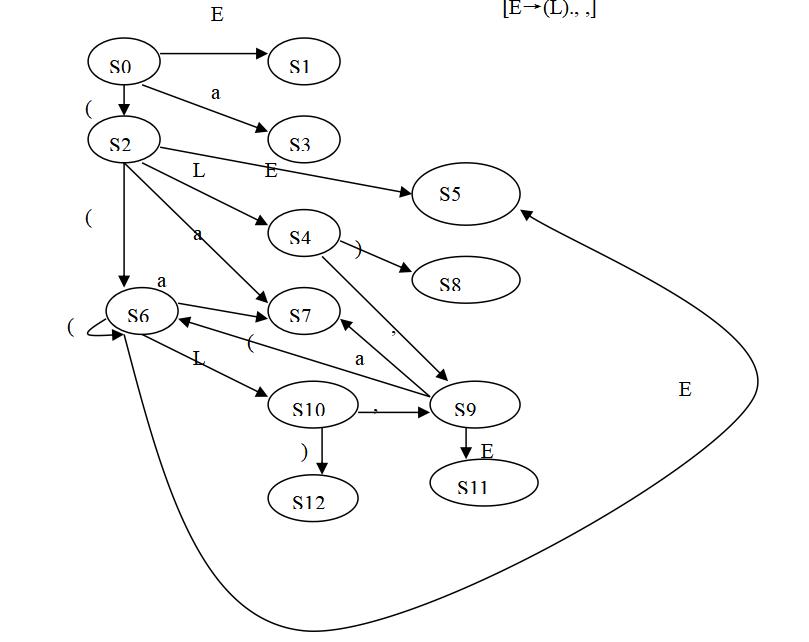
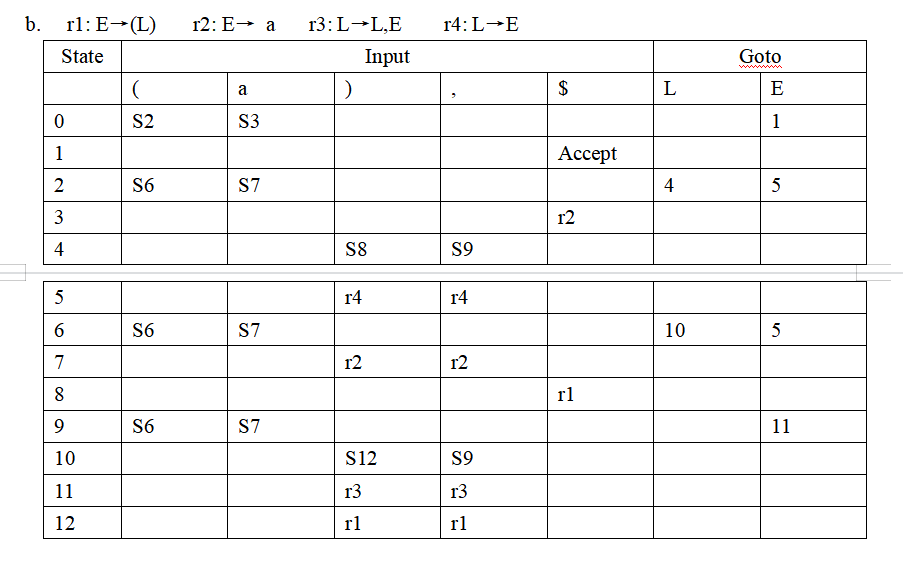

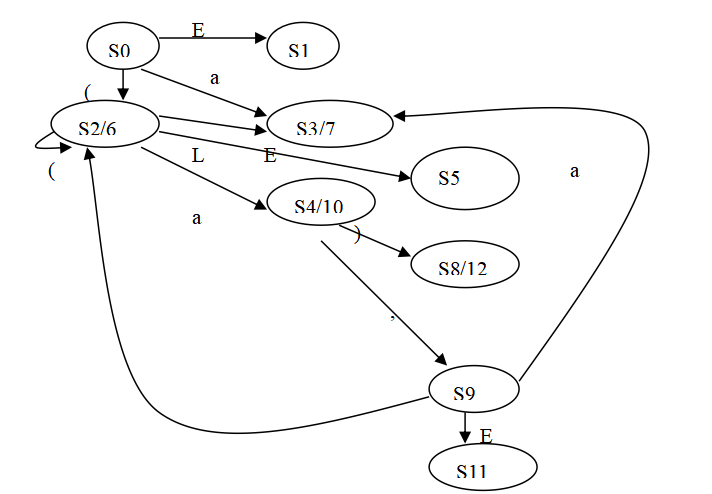
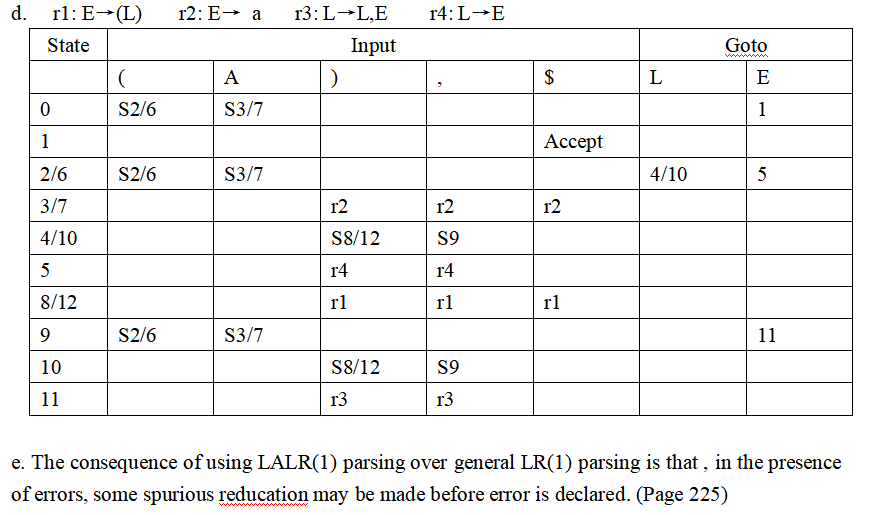
e. 使用 LALR(1) 解析而不是一般的 LR(1) 解析的结果是,在存在错误的情况下,可能会在声明错误之前进行一些虚假的规约。
语义分析
属性文法
构造属性文法
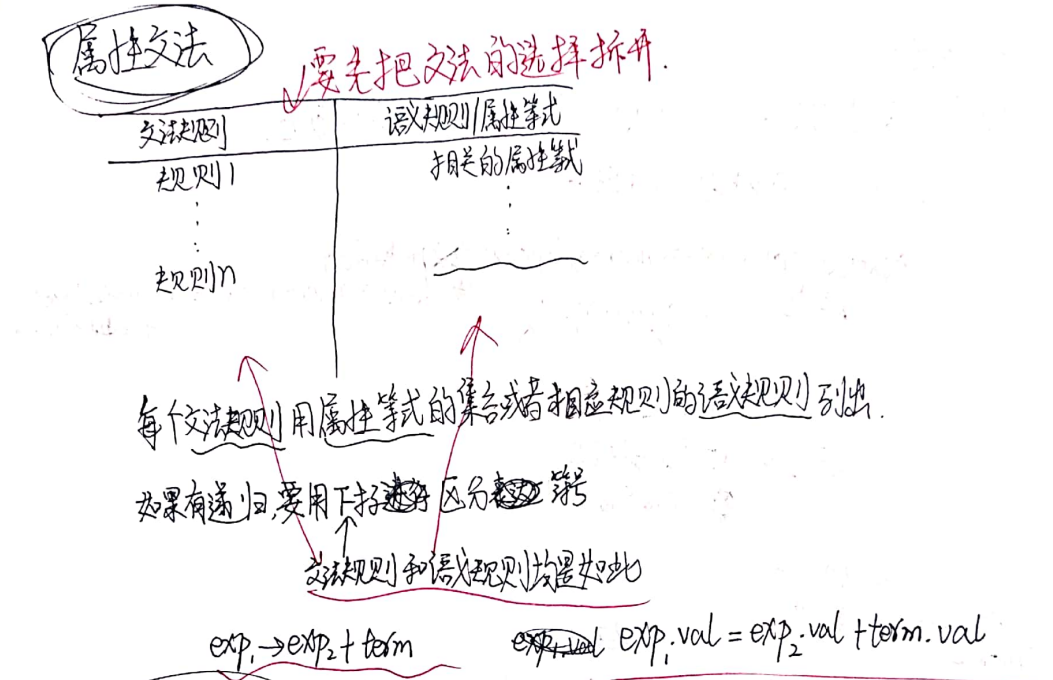
分析树
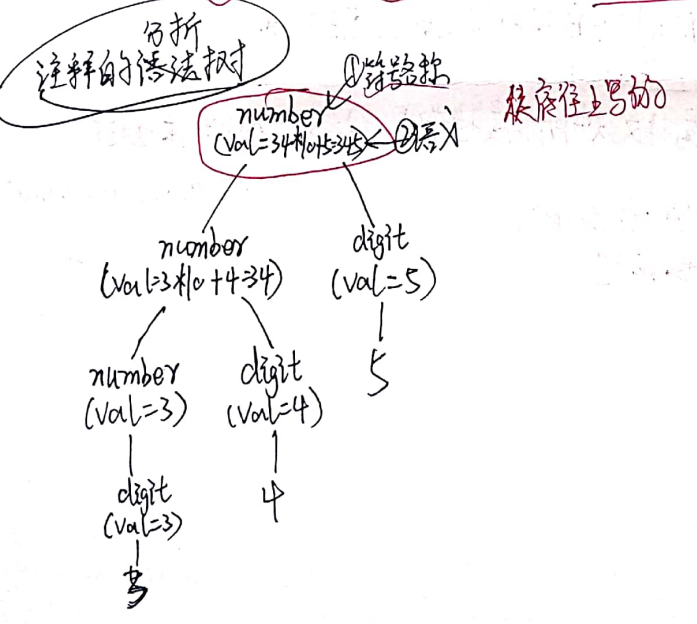
题:构造属性文法


题:分析树
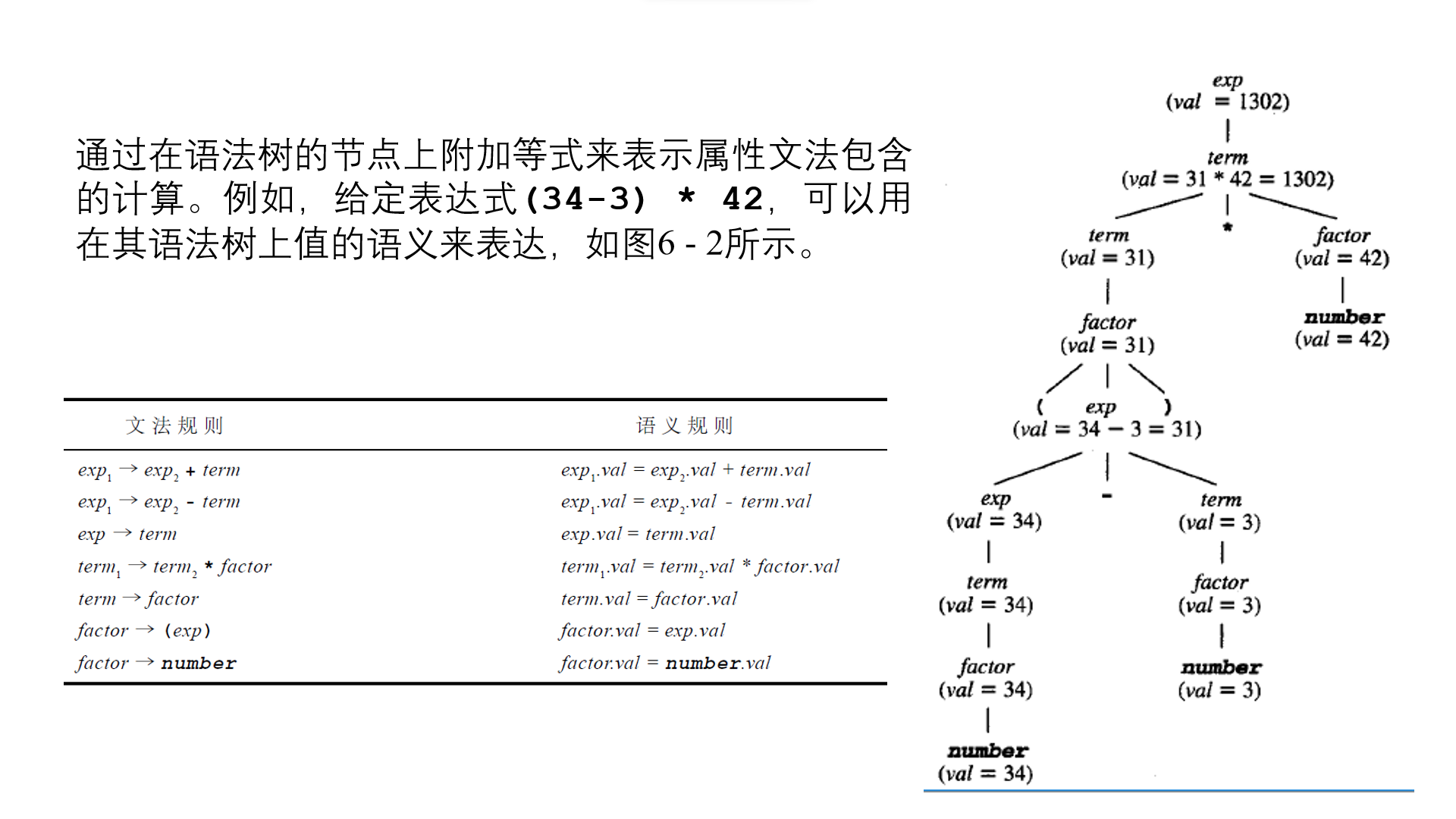
题:有数据类型的文法

题:有不同进制的文法
注意 if 语句错误判断


