数据结构与算法 期末复习

zstu 浙江理工大学 2023学年第1学期 数据结构与算法

huffman 带权路径长度 WPL: 路径长度 * 点的权值

prim: 在已确定生成树的相邻边找最小的
kruskal: 边按权值升序，依次选中，不能形成环

dijkstra: 每轮确定一个距离源点最短的点
floyd: 对于每一对顶点，尝试通过另一个顶点查找更短路径

Hash 失败查找长度：表内所有项都要计算(?) 直到找到空的次数

程序填空注意 T==NULL 的情况
树->二叉树：兄弟相连；取左孩子

第 1 章 绪论

1.2 算法和算法评价

1.2.2 性能指标

image-20240106223235275

image-20240106223255598

image-20240106223327553

第 2 章 线性表

2.2 顺序表示

内容略

题目

假设顺序表的长度为 n，

若在位序 1 处删除元素，则需要移动 n-1 个元素；

若在位序 n 处删除元素，则需要移动 0 个元素；

若在位序 i (1≤i≤n) 处删除元素，则需要移动 n-i 个元素。

假设各位序删除元素的概率相同，则平均需要移动 （n-1）/2 个元素。

假设顺序表的长度为 n，

若在位序 1 处插入元素，则需要移动 n 个元素；

若在位序 n+1 处插入元素，则需要移动 0 个元素；

若在位序 i (1≤i≤n+1) 处插入元素，则需要移动 n-i+1 个元素。

假设各位序插入元素的概率相同，则平均需要移动 n/2 个元素。

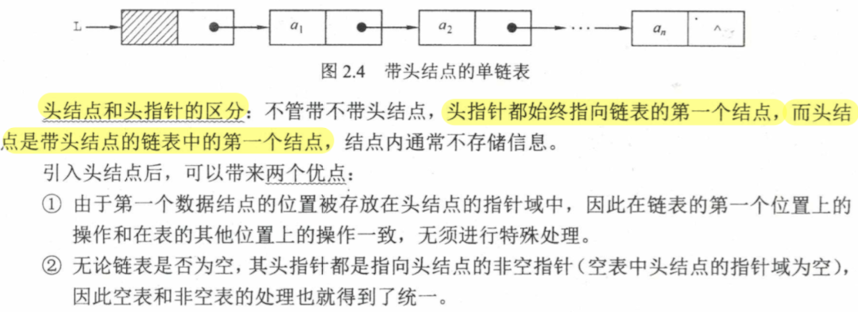
2.3 链式表示

2.3.1 定义

typedef struct LNode{
    int data;
    struct LNode* next;
}LNode, *LinkList;

image-20240106225208023

image-20240106225241311

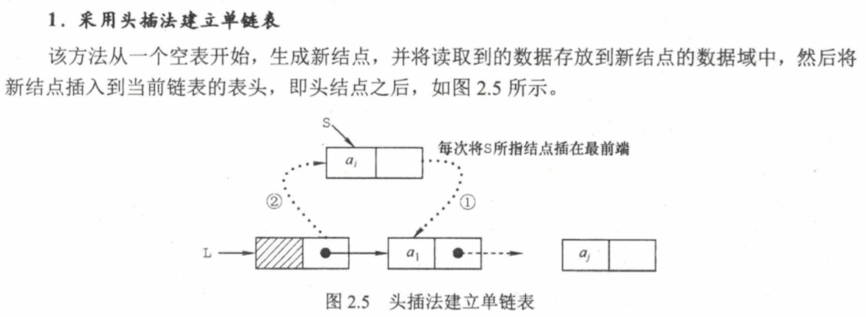
2.3.2 单链表操作

头插法

image-20240106225325940

LinkList headInsert(Linklist &L){
    LNode *s; int x;
    L = (LinkList)malloc(sizeof(LNode)); // 创建头结点
    L -> next = NULL;
    while(scanf("%d", &x)){
        s = (LNode*)malloc(sizeof(LNode)); // 创建新结点
        s -> data = x;
        s -> next = L -> next, L -> next = s;
    }
    return L;
}

image-20240106225918249

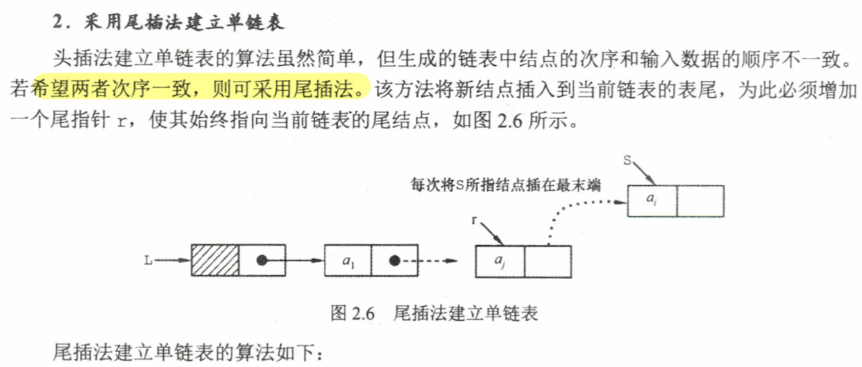
尾插法

image-20240106230006995

LinkList tailInsert(LinkList &L){
    int x;
    L = (LinkList)malloc(sizeof(LNode)); // 创建头结点
    LNode *newNode, *tail = L; // r是尾指针
    L -> next = NULL;
    while(scanf("%d", &x)){
        newNode = (LNode*)malloc(sizeof(LNode)); // 创建新结点
        newNode -> data = x;
        tail -> next = newNode, tail = newNode;
    }
    tail -> next = NULL;
    return L;
}
按序号查找

image-20240106231438391

LNode* getElem(LinkList L, int k){
    if(k < 1) return NULL;
    LNode* p = L -> next;
    for(int i = 1; i <= k; i++){
        if(p != NULL) p = p -> next;
    }
    retun p;
}
按值查找
LNode* findElem(LinkList L, int x){
    LNode* p = L -> next;
    while(p != NULL && p -> data != x) p = p -> next;
    return p;
}
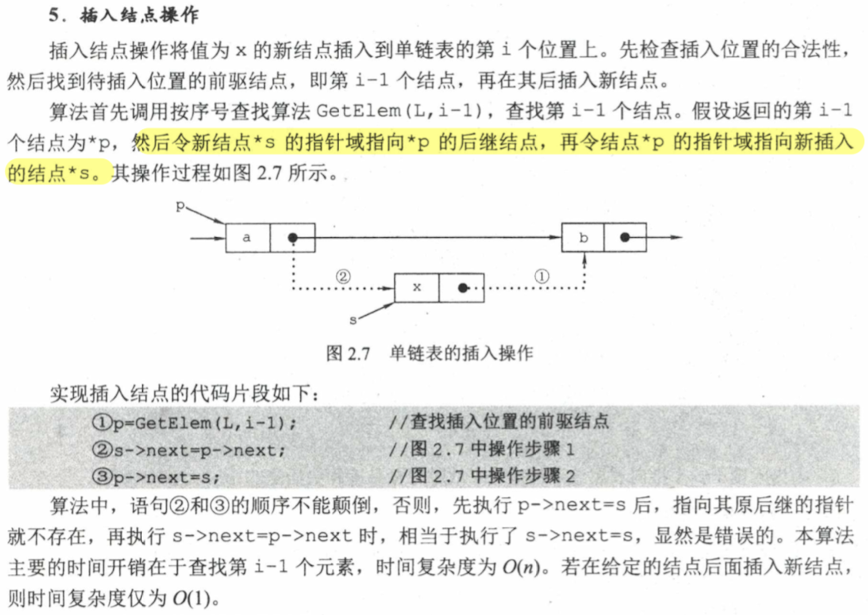
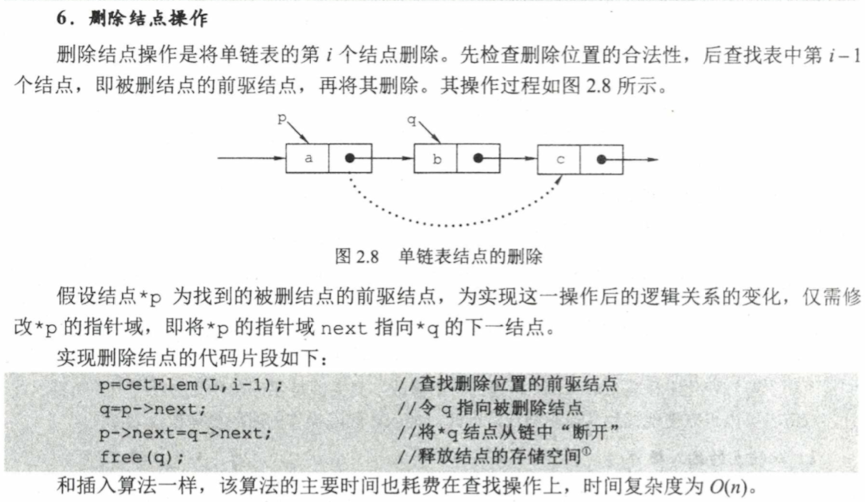
插入结点

image-20240106231829083

删除结点

image-20240106232319175

题目

image-20240108120832297

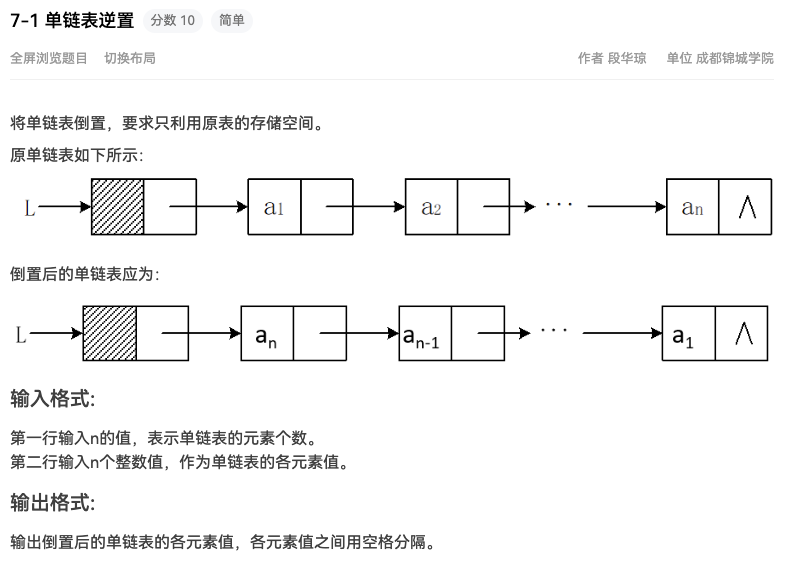
image-20240108124850376

image-20240108124915316

// 方法一
Node* reverseLinkedListMethod1(Node* head) {
    Node* prev = NULL;
    Node* current = head;
    Node* next;
    while (current != NULL) {
        next = current->next;
        current->next = prev;            // 反转当前节点
        prev = current, current = next;  // 两个指针前进一次
    }
    return prev;  // 反转后的链表的头节点
}

// 方法二
Node* reverseLinkedListMethod2(Node* head) {
    if (head == NULL || head->next == NULL) return head;  // 只有0或1个节点
    Node* newHead = reverseLinkedListMethod2(head->next);  // 反转剩余部分
    head->next->next = head;                               // 反转头节点
    head->next = NULL;
    return newHead;
}

第 3 章 栈、队列和数组

3.1 栈

image-20240106232511298

image-20240106232530724

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100  // 定义栈的最大容量

// 栈的结构定义
typedef struct {
    int items[MAX_SIZE];
    int top;
} Stack;

// 初始化栈
void initializeStack(Stack *s) {
    s->top = -1;
}

// 检查栈是否为空
int isEmpty(Stack *s) {
    return s->top == -1;
}

// 检查栈是否已满
int isFull(Stack *s) {
    return s->top == MAX_SIZE - 1;
}

// 推入操作
void push(Stack *s, int item) {
    if (isFull(s)) {
        printf("栈已满，无法添加元素\n");
        return;
    }
    s->items[++s->top] = item;
}

// 弹出操作
int pop(Stack *s) {
    if (isEmpty(s)) {
        printf("栈为空，无法弹出元素\n");
        return -1;  // 返回-1表示栈为空
    }
    return s->items[s->top--];
}

// 主函数
int main() {
    Stack s;
    initializeStack(&s);

    push(&s, 10);
    push(&s, 20);
    push(&s, 30);

    printf("弹出的元素：%d\n", pop(&s));
    printf("弹出的元素：%d\n", pop(&s));

    return 0;
}

3.2 队列

image-20240106232719626

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100  // 定义队列的最大容量

// 队列的结构定义
typedef struct {
    int items[MAX_SIZE];
    int front, rear;
} Queue;

// 初始化队列
void initializeQueue(Queue *q) {
    q->front = -1;
    q->rear = -1;
}

// 检查队列是否为空
int isEmpty(Queue *q) {
    return q->rear == -1;
}

// 检查队列是否已满
int isFull(Queue *q) {
    return q->rear == MAX_SIZE - 1;
}

// 入队操作
void enqueue(Queue *q, int item) {
    if (isFull(q)) {
        printf("队列已满，无法添加元素\n");
        return;
    }
    if (isEmpty(q)) {
        q->front = 0;
    }
    q->rear++;
    q->items[q->rear] = item;
}

// 出队操作
int dequeue(Queue *q) {
    if (isEmpty(q)) {
        printf("队列为空，无法弹出元素\n");
        return -1;  // 返回-1表示队列为空
    }
    int item = q->items[q->front];
    q->front++;
    if (q->front > q->rear) {
        // 重置队列
        initializeQueue(q);
    }
    return item;
}

// 主函数
int main() {
    Queue q;
    initializeQueue(&q);

    enqueue(&q, 10);
    enqueue(&q, 20);
    enqueue(&q, 30);

    printf("出队的元素：%d\n", dequeue(&q));
    printf("出队的元素：%d\n", dequeue(&q));

    return 0;
}

3.4 数组和特殊矩阵

3.4.3 特殊矩阵的压缩存储

对称矩阵

image-20240106233056953

image-20240106233105257

三角矩阵

image-20240106233209992

image-20240106233227002

题目

image-20240108125706878

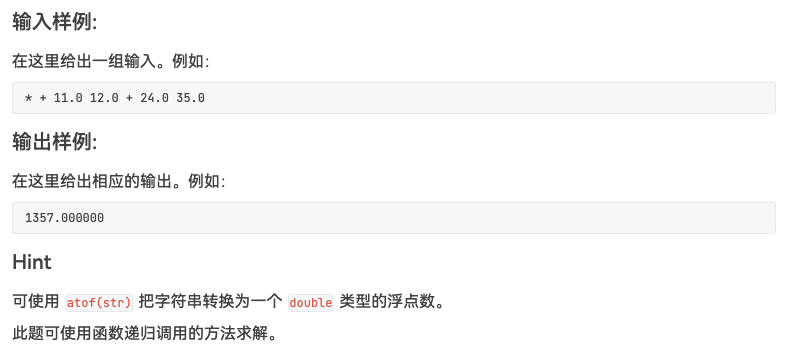
image-20240108125716455

double eval() {
    char s[100];
    scanf("%s", s);
    // 根据读取的字符串判断是操作符还是操作数
    switch (s[0]) {
        case '+': return eval() + eval();
        case '-': return eval() - eval();
        case '*': return eval() * eval();
        case '/': return eval() / eval();
        case '^': {
            double base = eval();
            double exp = eval();
            return pow(base, exp);
        }
        default: return atof(s); // 将字符串转换为浮点数
    }
}

第 5 章 树与二叉树

5.1 树的概念

5.1.1 定义

image-20240106152037942

image-20240106152055920

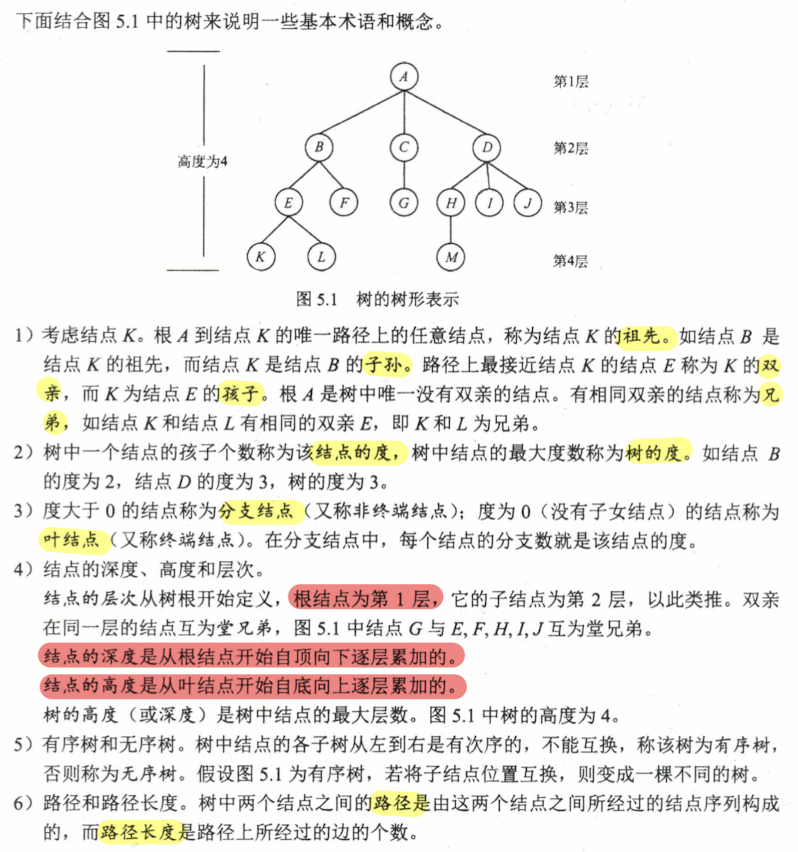
5.1.2 术语

image-20240106152553967

image-20240106152621444

image-20240106152631181

5.1.3 性质

image-20240106152737658

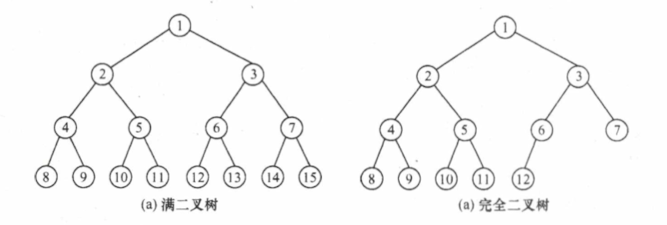
5.2 二叉树的概念

5.2.1 定义 性质

定义

image-20240106152921545

image-20240106153138908

性质

image-20240106153501857

image-20240106153512895

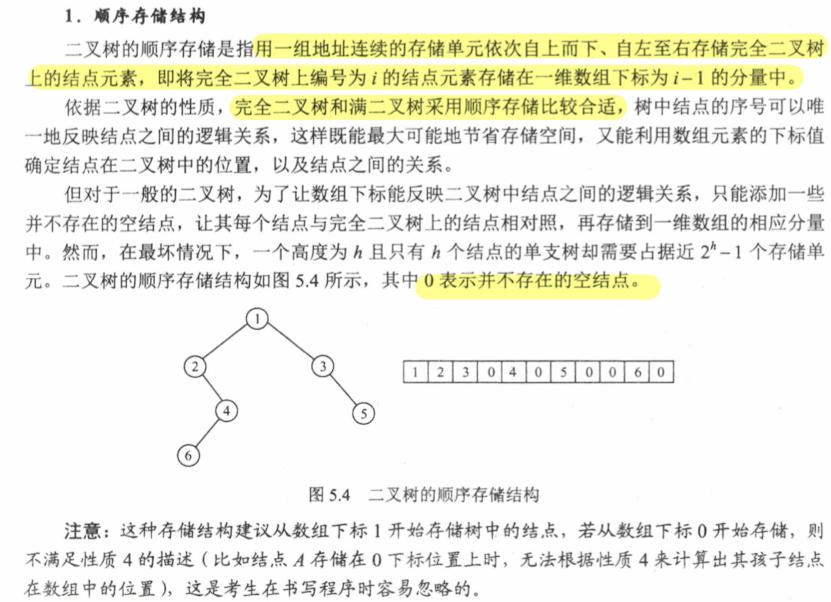
5.2.2 存储结构

顺序

image-20240106153730560

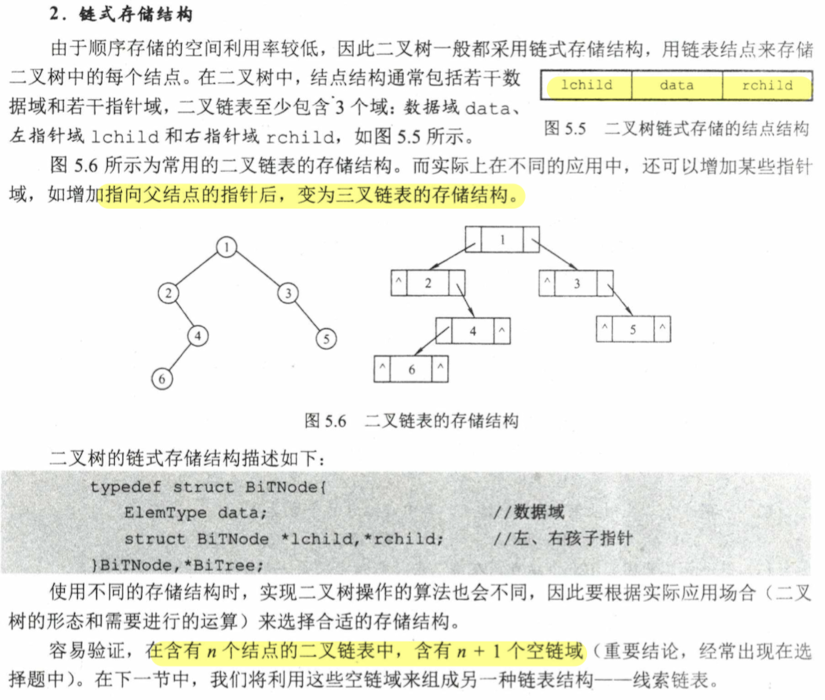
链式
typedef struct TreeNode{
    int data;
    struct TreeNode *left, *right;
} TreeNode, *Tree;

image-20240106153933064

题目

image-20240107094249909

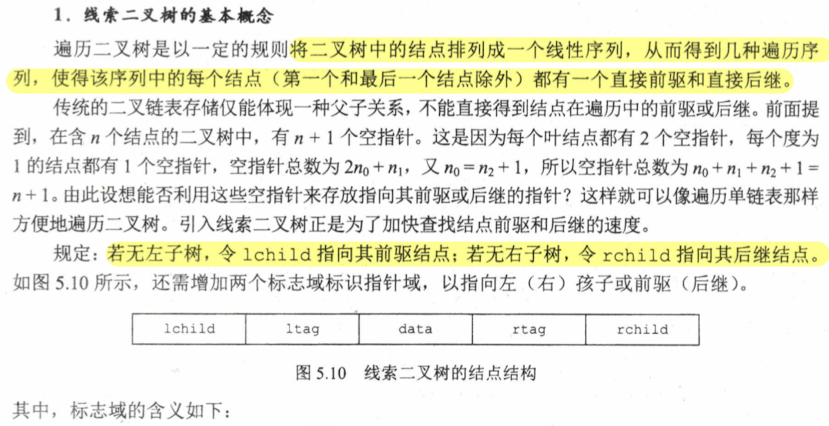
5.3 二叉树的遍历 线索二叉树

要求掌握求二叉树深度的代码，判断是否为满二叉树的代码

// 计算二叉树的最大深度
int maxDepth(TreeNode* root) {
    if (root == NULL) {
        return 0;
    }
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);
    return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}

// 计算二叉树的节点数
int countNodes(TreeNode* root) {
    if (root == NULL) {
        return 0;
    }
    return 1 + countNodes(root->left) + countNodes(root->right);
}

// 判断是否为满二叉树
int isFullBinaryTree(TreeNode* root) {
    int depth = maxDepth(root);
    int nodes = countNodes(root);
    return nodes == (1 << depth) - 1;
}

5.3.1 二叉树的遍历

先序

void PreOrder(Tree T){
    if(T != NULL){
        visit(T);
        PreOrder(T -> left);
        PreOrder(T -> right);
    }
}

中序

void InOrder(Tree T){
    if(T != NULL){
        InOrder(T -> left);
        visit(T);
        InOrder(T -> right);
    }
}

后序

void PostOrder(Tree T){
    if(T != NULL){
        PostOrder(T -> left);
        PostOrder(T -> right);
        visit(T);
    }
}

5.3.2 线索二叉树*

image-20240106155200913

image-20240106155215156

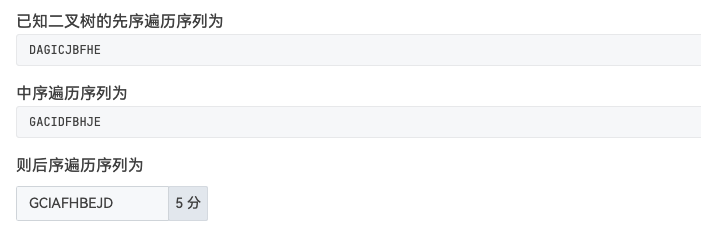
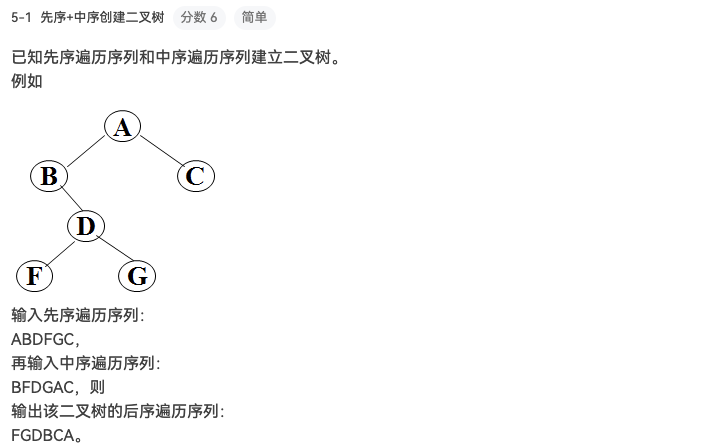
题目

对于前序、中序找后序，树的结点确定顺序=前序

image-20240107094239772

image-20240107094349243

image-20240107094356481

image-20240107094403828

image-20240107094546256

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef char ElementType;
typedef struct BiTNode {
    ElementType data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

BiTree CreatBinTree(char *pre, char *in, int n);
void postorder(BiTree T);

int main() {
    BiTree T;
    char prelist[100];
    char inlist[100];
    int length;
    scanf("%s", prelist);
    scanf("%s", inlist);
    length = strlen(prelist);
    T = CreatBinTree(prelist, inlist, length);
    postorder(T);
    return 0;
}
void postorder(BiTree T) {
    if (T) {
        postorder(T->lchild);
        postorder(T->rchild);
        printf("%c", T->data);
    }
}
BiTree CreatBinTree(char *pre, char *in, int n) {
    BiTree T;
    int i;
    if (n <= 0) return NULL;
    T = (BiTree)malloc(sizeof(BiTNode));
    T->data = pre[0];
    for (i = 0; in[i] != pre[0]; i++)
        ;
    T->lchild = CreatBinTree(pre + 1, in, i); // 程序填空
    T->rchild = CreatBinTree(pre + i + 1, in + i + 1, n - i - 1); // 程序填空
    return T;
}

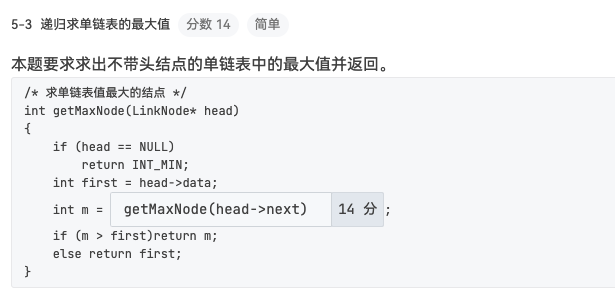
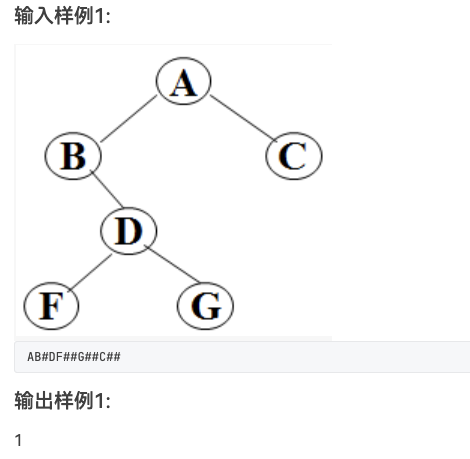
统计二叉树度为1的结点个数。

image-20240107094948176

#include <iostream>
using namespace std;
typedef struct BiNode {
    char data;
    struct BiNode *lchild, *rchild;
} BiTNode, *BiTree;

void CreateBiTree(BiTree &T) {
    char ch;
    cin >> ch;
    if (ch == '#')
        T = NULL;
    else {
        T = new BiTNode;
        T->data = ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}

int NodeCount(BiTree T) {
    if (T == NULL) return 0;  // 程序填空
    if (T->lchild == NULL && T->rchild != NULL)
        return 1 + NodeCount(T->rchild);  // 程序填空
    if (T->lchild != NULL && T->rchild == NULL)
        return 1 + NodeCount(T->lchild);                 // 程序填空
    return NodeCount(T->lchild) + NodeCount(T->rchild);  // 程序填空
}

int main() {
    BiTree T;
    CreateBiTree(T);
    printf("%d", NodeCount(T));
    return 0;
}

计算二叉树深度。

#include <iostream>
using namespace std;

typedef struct BiNode {
    char data;
    struct BiNode *lchild, *rchild;
} BiTNode, *BiTree;

void CreateBiTree(BiTree &T) {
    char ch;
    cin >> ch;
    if (ch == '#')
        T = NULL;
    else {
        T = new BiTNode;
        T->data = ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}

int Depth(BiTree T) {
    int m, n;
    if (T == NULL) // 程序填空
        return 0;
    else {
        m = Depth(T->lchild); // 程序填空
        n = Depth(T->rchild); // 程序填空
        if (m > n)
            return (m + 1);
        else
            return (n + 1);
    }
}

int main() {
    BiTree tree;
    CreateBiTree(tree);
    cout << Depth(tree);
    return 0;
}

image-20240108151108738

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode {
    int value;
    struct TreeNode *left, *right;
} TreeNode;

TreeNode* buildTree(int* preorder, int* inorder, int inorderStart, int inorderEnd) {
    static int preorderIndex = 0;
    if (inorderStart > inorderEnd) return NULL;

    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->value = preorder[preorderIndex++];
    node->left = node->right = NULL;

    if (inorderStart == inorderEnd) return node;

    int inorderIndex;
    for (inorderIndex = inorderStart; inorderIndex <= inorderEnd; inorderIndex++) {
        if (inorder[inorderIndex] == node->value) break;
    }

    node->left = buildTree(preorder, inorder, inorderStart, inorderIndex - 1);
    node->right = buildTree(preorder, inorder, inorderIndex + 1, inorderEnd);

    return node;
}

void mirrorTree(TreeNode* root) {
    if (root == NULL) return;

    TreeNode* temp = root->left;
    root->left = root->right;
    root->right = temp;

    mirrorTree(root->left);
    mirrorTree(root->right);
}

void levelOrderTraversal(TreeNode* root, int n) {
    if (root == NULL) return;

    TreeNode **queue = (TreeNode**)malloc(n * sizeof(TreeNode*));
    int front = 0, rear = 0, count = 0;

    queue[rear++] = root;
    while (front < rear) {
        TreeNode* current = queue[front++];
        printf("%d", current->value);
        if (++count < n) printf(" ");
        if (current->left) queue[rear++] = current->left;
        if (current->right) queue[rear++] = current->right;
    }

    free(queue);
}


int main() {
    int n;
    scanf("%d", &n);
    int inorder[n], preorder[n];

    for (int i = 0; i < n; i++) {
        scanf("%d", &inorder[i]);
    }
    for (int i = 0; i < n; i++) {
        scanf("%d", &preorder[i]);
    }

    TreeNode* root = buildTree(preorder, inorder, 0, n - 1);
    mirrorTree(root);
    levelOrderTraversal(root, n);

    return 0;
}

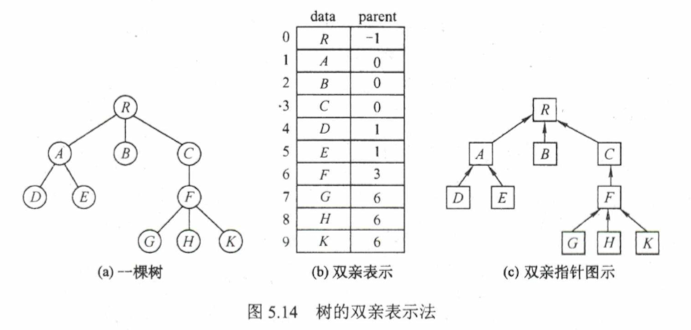
5.4 树 森林

5.4.1 树的存储结构

双亲表示法

image-20240106155520855

image-20240106155539041

typedef struct Node{
    int data;
    int parent; //父节点在数组中的位置
}Node;
typedef struct Tree{
    Node nodes[100];
    int n; //节点数
}Tree;
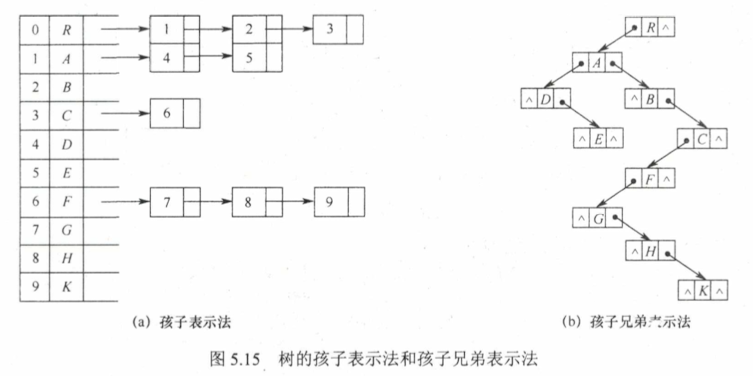
孩子表示法

image-20240106160017112

image-20240106160029455

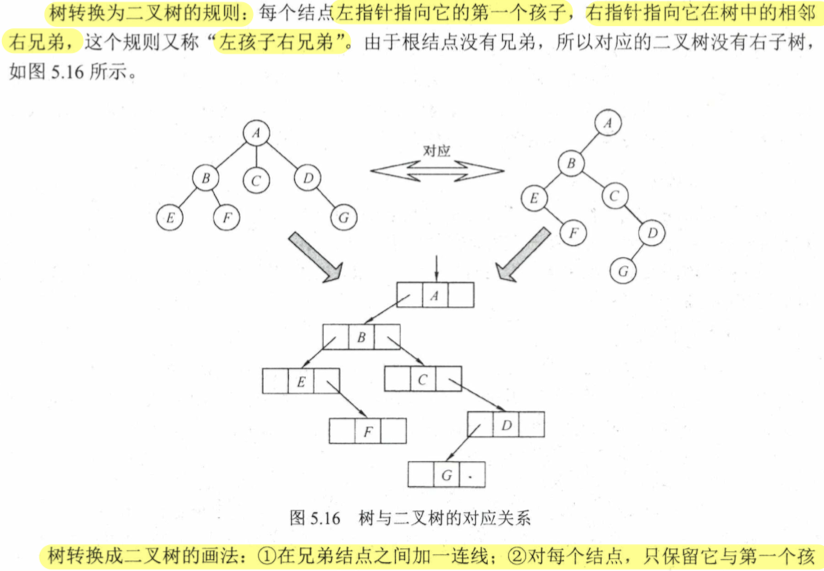
孩子兄弟表示法

此方法就是将树转换为二叉树的方法

image-20240106160150307

typedef struct Node{
    int data;
    struct Node *firstChild, *next Sibling;//结点的第一个孩子, 结点的右兄弟
}

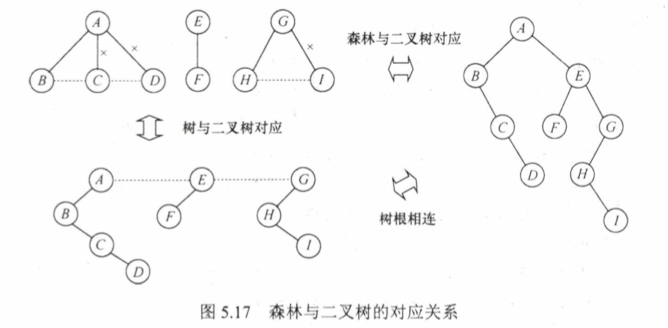
5.4.2 转换

树->二叉树

image-20240106161008260

image-20240106161721167

森林->二叉树

image-20240106161735509

image-20240106161814832

二叉树->森林

image-20240106162050164

5.4.3 遍历

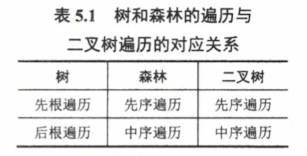
image-20240106162307235

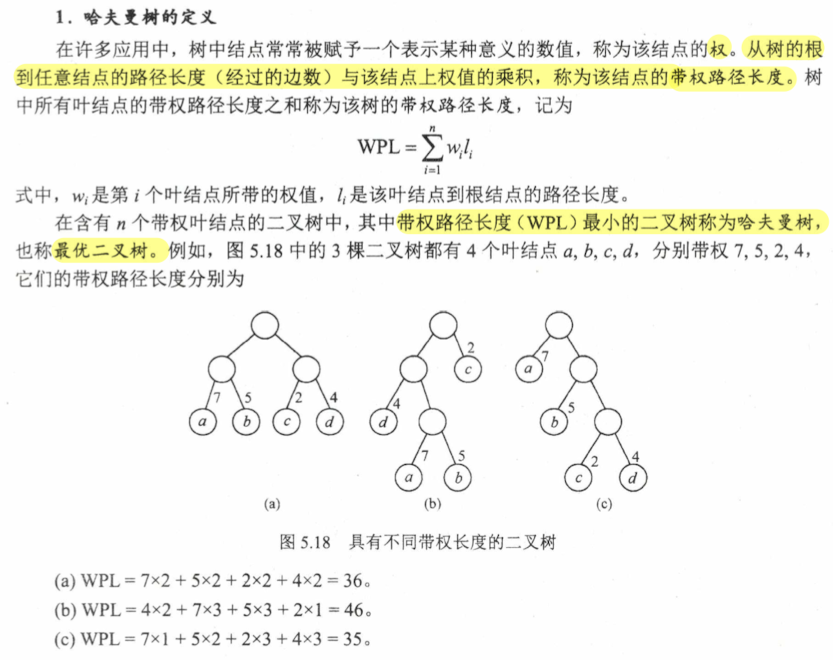
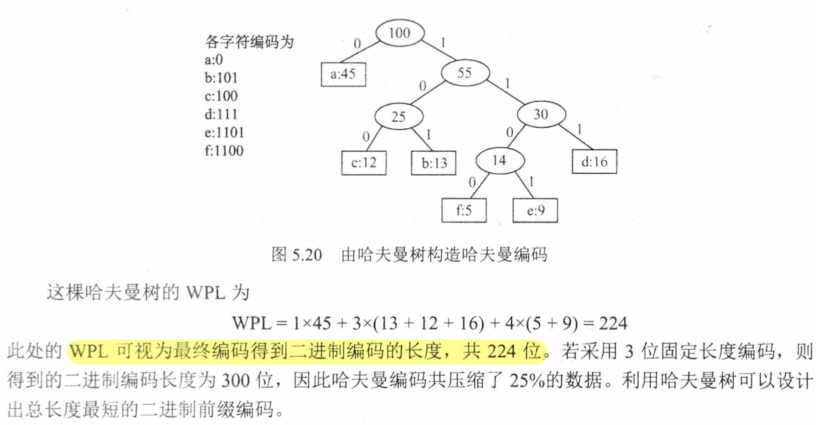
5.5 应用

5.5.1 哈夫曼树 哈夫曼编码

定义

image-20240106162631634

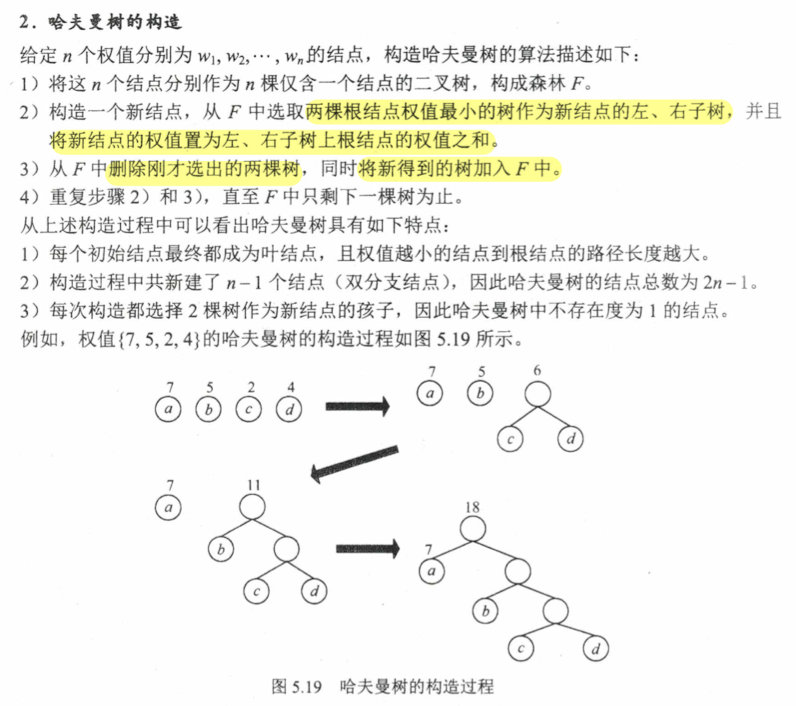
构造

image-20240106162803726

哈夫曼编码

是可变长度编码

是前缀编码（没有任何编码是另一个编码的前缀）

image-20240106163116722

5.5.2 并查集

它支持两种操作：

  1. 查找（Find）：确定某个元素属于哪个子集。
  2. 合并（Union）：将两个子集合并成一个集合。

parent[i] 表示元素 i 的父节点

int parent[100];
void init(int n){
    for(int i = 0; i < n; i++)
        parent[i] = i;
}
int find(int x){
    if(parent[x] == x) return x;
    return find(parent[x]);
}
void unionSets(int x, int y){
    int xRoot = find(x), yRoot = find(y);
    if(xRoot != yRoot) parent[xRoot] = yRoot;// 将x的根节点的父节点设置为y的根节点
}

第 6 章 图

6.1 概念

概念参考 离散数学 期末复习 第5章

题目

在有n个顶点的有向图中，若要使任意两点间可以互相到达，则至少需要 n 条弧

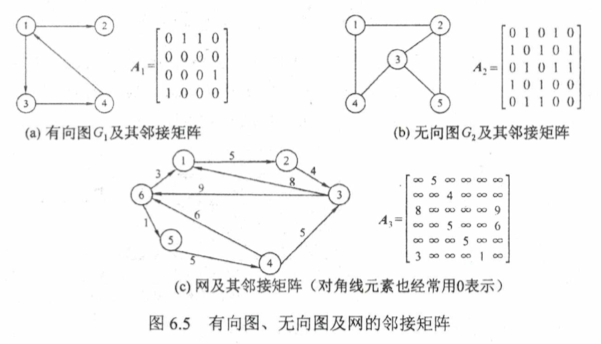
6.2 存储结构和操作

6.2.1 邻接矩阵

image-20240106170056641

image-20240106170218669

image-20240106170226436

typedef struct Graph{
    int V[MAXN]; // 顶点
    int Edge[MAXN][MAXN]; // 邻接矩阵
    int n, m; // 顶点数, 边数
}Graph;

邻接矩阵的性质参考 离散数学 期末复习 第5章

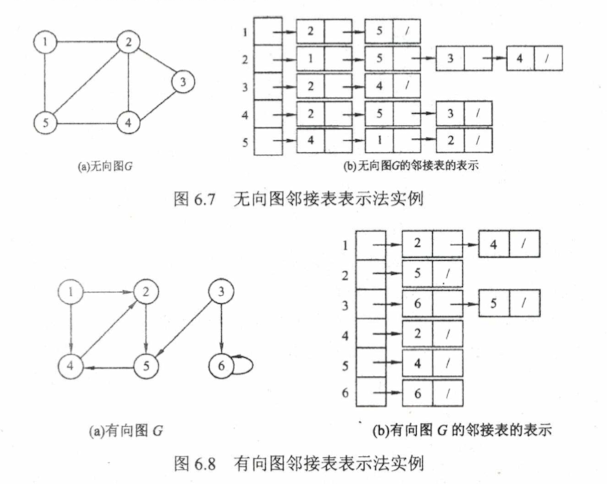
6.2.2 邻接表

image-20240106171153090

image-20240106171222481

typedef struct AdjListNode{ // 邻接表中链表的节点
    int dest; // 目标顶点
    struct AdjListNode* next;
}AdjListNode;
typedef struct AdjList{ // 邻接表
    int data;
    struct AdjListNode* head; // 链表头指针
}AdjList;
typedef struct Graph{
    int n, m; //顶点数, 边数
    struct AdjList* array; // 是一个数组, 数组的每个元素都是一个链表（邻接表）
}Graph;

image-20240106172634242

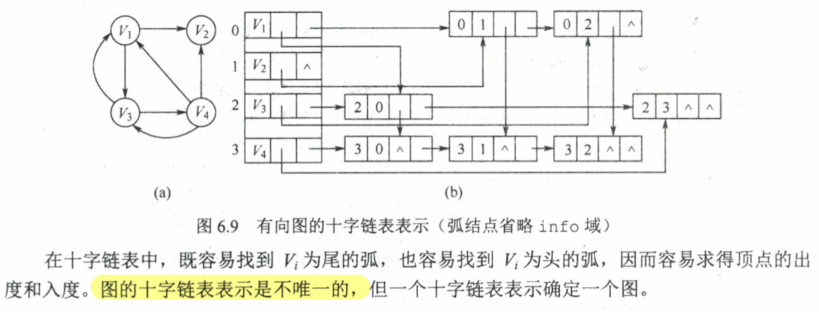
6.2.3 十字链表

注意弧头是有向边的终点，弧尾是有向边的起点

image-20240106172857905

image-20240106173238689

6.2.4 邻接多重表

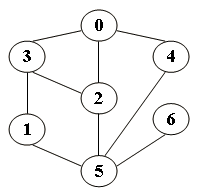
题目

要求建立一个无向图，采用邻接表做为存储结构。
例如

QQ截图20190522185944.png

输入信息为：第一行给出图的顶点数n和边数e。第二行给出n个字符，表示n个顶点的数据元素的值。后面是e行，给出每一条边的两个顶点编号。

输出每个顶点的值以及各顶点的邻接点的值。

输入样例为：
7 9
0123456
0 2
0 3
0 4
1 3
1 5
2 3
2 5
4 5
5 6

输出样例为
0: 4 3 2
1: 5 3
2: 5 3 0
3: 2 1 0
4: 5 0
5: 6 4 2 1
6: 5
#include <stdio.h>
#include <stdlib.h>
#define MVNum 100             // 最大顶点数
typedef struct ArcNode {      // 表结点
    int adjvex;               // 邻接点的位置
    struct ArcNode *nextarc;  // 指向下一个表结点的指针
} ArcNode;
typedef struct VNode {
    char data;            // 顶点信息
    ArcNode *firstarc;    // 指向第一个表结点的指针
} VNode, AdjList[MVNum];  // AdjList表示邻接表类型
typedef struct {
    AdjList vertices;    // 头结点数组
    int vexnum, arcnum;  // 图的当前顶点数和边数
} ALGraph;
void CreatMGraph(ALGraph *G); /* 创建图 */
void printGraph(ALGraph G);   /*输出图 */
int main() {
    ALGraph G;
    CreatMGraph(&G);
    printGraph(G);
    return 0;
}
void CreatMGraph(ALGraph *G) {
    int i, j, k;
    ArcNode *s;
    scanf("%d%d", &G->vexnum, &G->arcnum);
    getchar();
    for (i = 0; i < G->vexnum; i++) scanf("%c", &G->vertices[i].data); // 程序填空
    for (i = 0; i < G->vexnum; i++) G->vertices[i].firstarc = NULL; // 程序填空

    for (k = 0; k < G->arcnum; k++) {
        scanf("%d%d", &i, &j);
        
        s = (ArcNode *)malloc(sizeof(ArcNode));
        s->adjvex = j;
        s->nextarc = G->vertices[i].firstarc;
        G->vertices[i].firstarc = s; // 程序填空
        
        s = (ArcNode *)malloc(sizeof(ArcNode));
        s->adjvex = i;
        s->nextarc = G->vertices[j].firstarc; // 程序填空
        G->vertices[j].firstarc = s; // 程序填空
    }
}
void printGraph(ALGraph G) {
    int i, j;
    ArcNode *p;
    for (i = 0; i < G.vexnum; i++) {
        printf("%c:", G.vertices[i].data);
        for (p = G.vertices[i].firstarc; p; p = p->nextarc)
            printf(" %c", G.vertices[p->adjvex].data);
        printf("\n");
    }
}

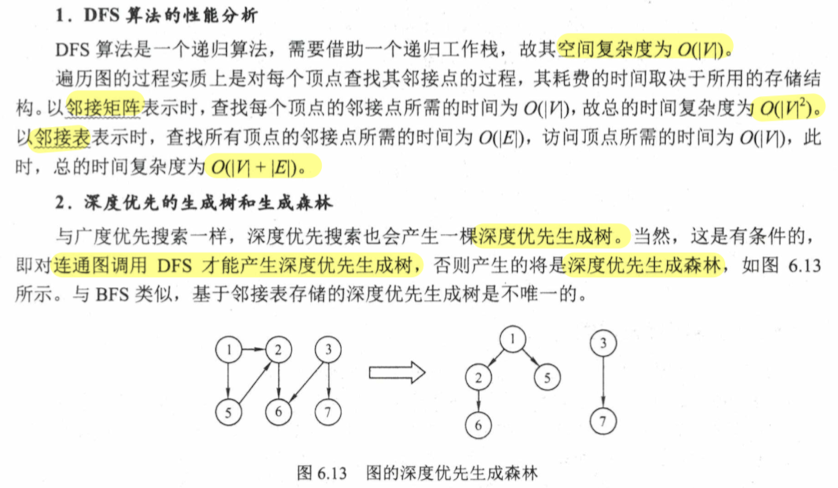
6.3 遍历

6.3.1 广度优先搜索 BFS

可能要求代码实现

image-20240106173834550

image-20240106173958059

image-20240106174102528

6.3.2 深度优先搜索 DFS

可能要求代码实现

image-20240106174200003

image-20240106174248591

image-20240106174326494

6.3.3 连通性

image-20240106183631606

image-20240106183637806

题目

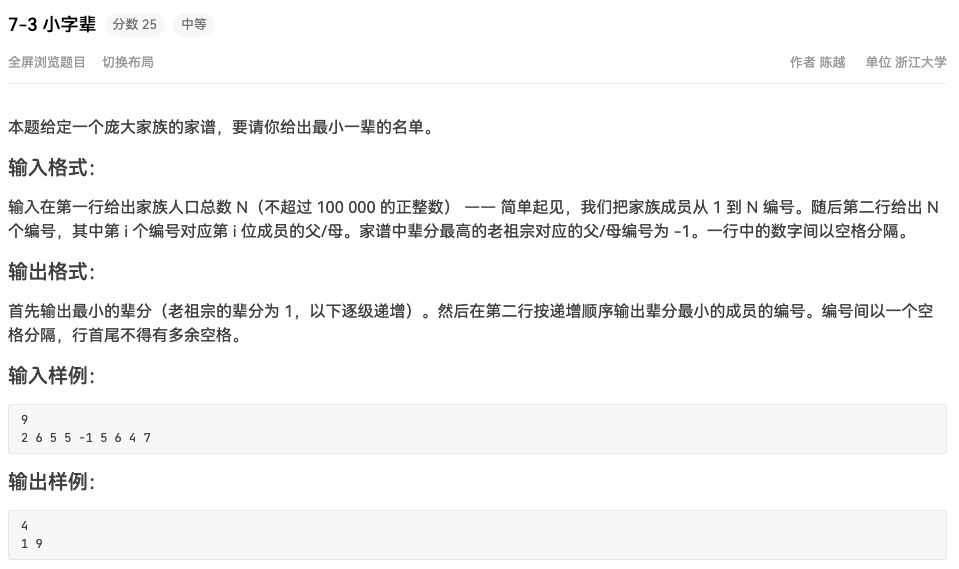
image-20240108152116294

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct peo{
    int id, level;
};
int main(){
    int n, temp, maxlevel = -1;
    queue<peo> q;
    vector<peo> ans;
    cin >> n;
    vector<vector<int>> v(n+1);
    for(int i = 1; i <= n; i++) {
        cin >> temp;
        if(temp == -1) temp = 0;
        v[temp].push_back(i);
    }
    q.push({0,0});
    while(!q.empty()) {
        peo p  = q.front();
        int id = p.id, level = p.level;
        if(p.level > maxlevel) maxlevel = p.level;
        ans.push_back(p);
        q.pop();
        for(int i = 0; i < v[id].size(); i++)
            q.push({v[id][i], level + 1});
    }
    cout << maxlevel << endl;
    for(int i = 0; i < ans.size(); i++) {
        if(ans[i].level == maxlevel) {
            cout << ans[i].id;
            if(i != ans.size() - 1) cout << " ";
        }
    }
    return 0;
}

image-20240108152931339

题目链接：https://pintia.cn/problem-sets/994805046380707840/problems/994805061769609216

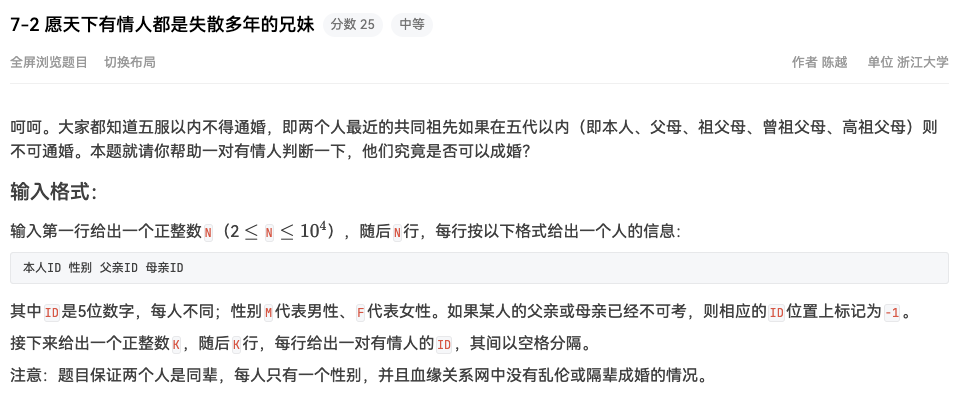
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int n;
struct people{
    int sex,father=-1,mother=-1;
}peo[N];
bool st[N],flag;
void dfs(int cur,int generation)
{
    if(cur==-1) return;
    if(generation>5) return;
    st[cur]=1;
    dfs(peo[cur].father,generation+1);
    dfs(peo[cur].mother,generation+1);
}
void finddfs(int cur,int generation)
{
    if(cur==-1) return;
    if(generation>5) return;
    if(st[cur]) flag=true;
    finddfs(peo[cur].father,generation+1);
    finddfs(peo[cur].mother,generation+1);
}
int main()
{
    cin>>n;
    int id,father,mother;
    string sex;
    for(int i=0;i<n;i++)
    {
        cin>>id>>sex;
        if(sex=="M") peo[id].sex=1;
        else peo[id].sex=0;
        cin>>peo[id].father>>peo[id].mother;
        peo[peo[id].father].sex=1;
        peo[peo[id].mother].sex=0;  
    }
    cin>>n;
    int a,b;
    for(int i=0;i<n;i++)
    {
        cin>>a>>b;
        if(peo[a].sex==peo[b].sex) puts("Never Mind");
        else{
            memset(st,false,sizeof st);
            dfs(a,1);
            flag=false;
            finddfs(b,1);
            if(flag) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}

作者：GRID
链接：https://www.acwing.com/solution/content/21635/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

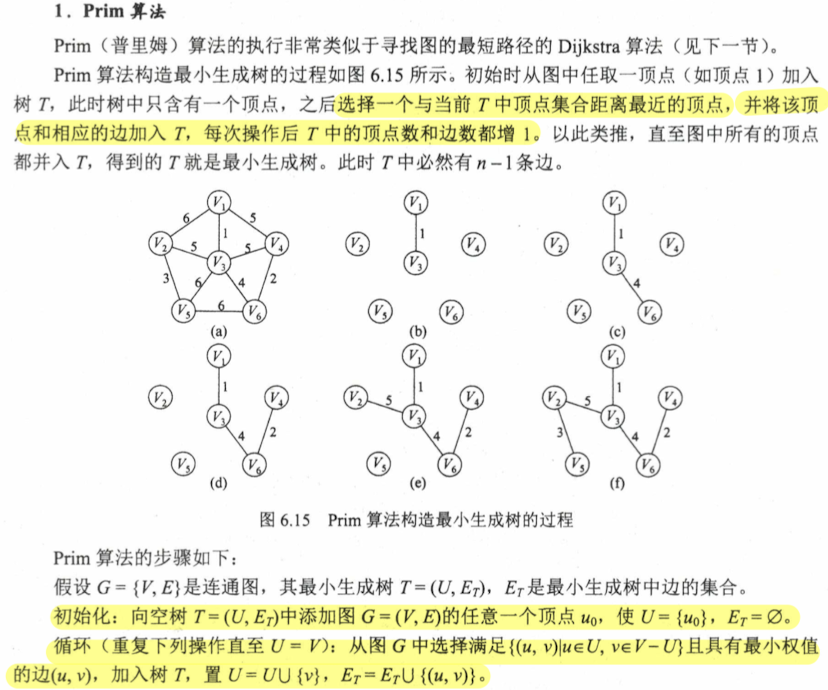
6.4 应用

6.4.1 最小生成树

image-20240106184516208

image-20240106184525755

image-20240106184532707

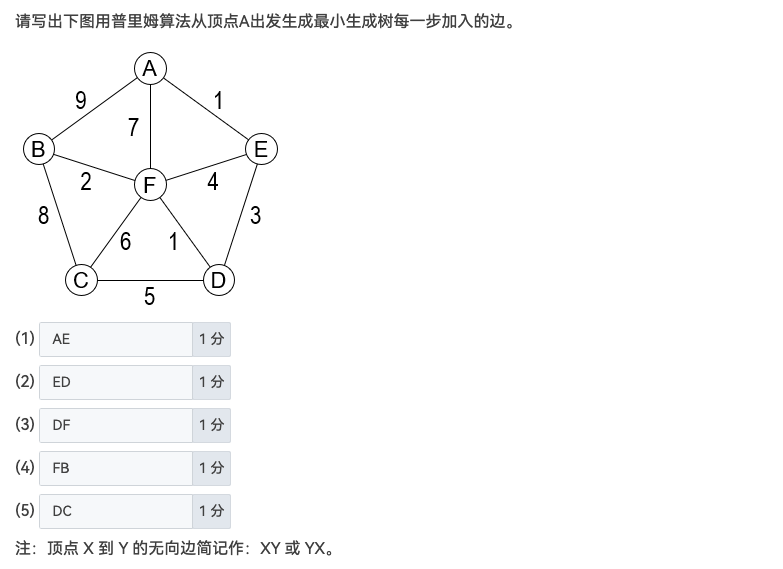
Prim 算法

可能要求代码实现

image-20240108165427899

image-20240106184754723

image-20240106184812260

Kruskal 算法

可能要求代码实现

image-20240108165750005

image-20240106185859320

image-20240106185907417

image-20240106185913942

// 查找根节点
int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

// 将元素x和元素y所在的集合合并
void union_set(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        if (ranks[rootX] < ranks[rootY]) {
            parent[rootX] = rootY;
        } else if (ranks[rootX] > ranks[rootY]) {
            parent[rootY] = rootX;
        } else {
            parent[rootY] = rootX;
            ranks[rootX]++;
        }
    }
}

// 克鲁斯卡尔算法 最小生成树 用并查集判环
int kruskal() {
    int mst_cost = 0, edges_selected = 0;
    qsort(edges, M, sizeof(edges[0]), cmp);  // 对边按成本进行排序
    for (int i = 0; i < N; i++) {
        parent[i] = i;
        ranks[i] = 0;
    }
    for (int i = 0; i < M && edges_selected < N - 1; i++) {
        int u = edges[i].u;
        int v = edges[i].v;
        if (find(u) != find(v)) {  // 如果两个节点不在同一个集合中
            union_set(u, v);       // 合并两个集合
            mst_cost += edges[i].cost;  // 累加边的成本
            edges_selected++;           // 选中边数增加
        }
    }
    if (edges_selected != N - 1) {
        return -1;  // 无法连接所有村落
    }
    return mst_cost;  // 总成本
}

题目

image-20240108130137686

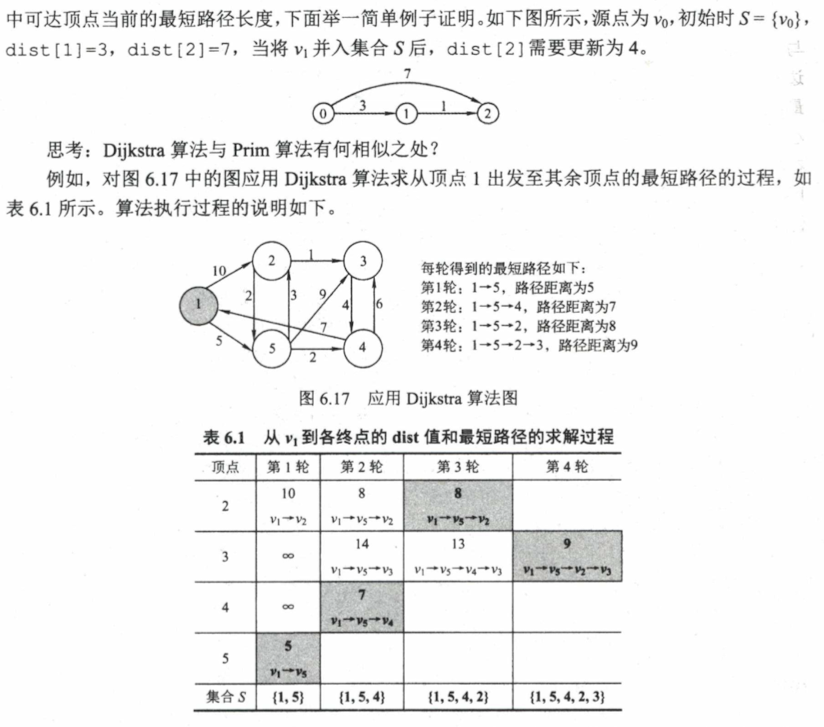
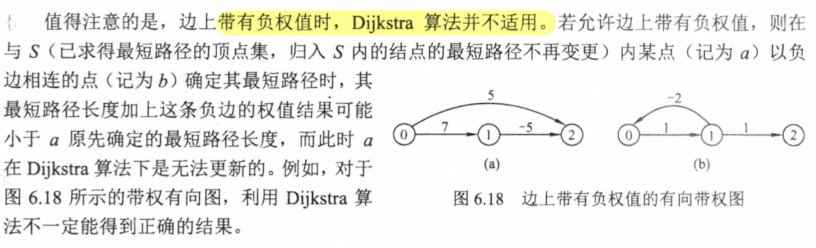
6.4.2 最短路径

Dijkstra 算法

不要求代码实现，要会画求解过程的表格

image-20240108164507695

image-20240106191316433

image-20240106191328945

image-20240106191337016

image-20240106191344060

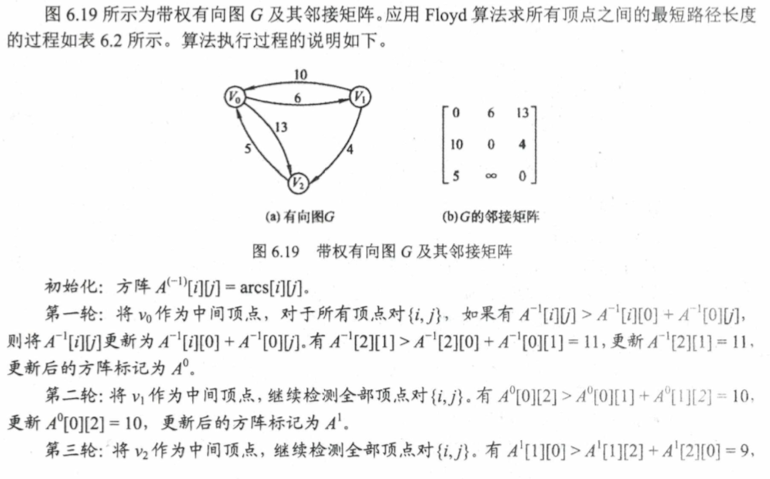
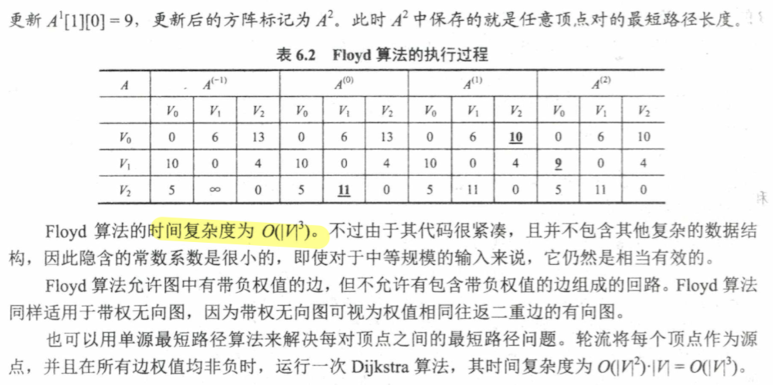
Floyd 算法

可能要求算法实现

image-20240108164902883

image-20240108150426346

image-20240108150433927

image-20240108150446933

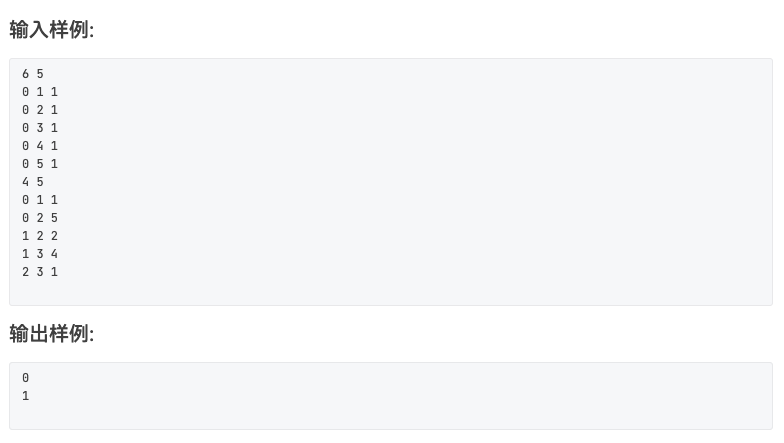
题目

image-20240108150513601

image-20240108150520805

#include <stdio.h>
#include <limits.h>

#define MAXN 100
#define INF INT_MAX

int n, e;
int dist[MAXN][MAXN];

// 初始化邻接矩阵
void initialize() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (i == j) dist[i][j] = 0;
            else dist[i][j] = INF;
        }
    }
}

// Floyd-Warshall算法
void floydWarshall() {
    for (int k = 0; k < n; k++) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (dist[i][k] != INF && dist[k][j] != INF && dist[i][j] > dist[i][k] + dist[k][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }
}

int main() {
    while (scanf("%d %d", &n, &e) != EOF) {
        initialize();
        int a, b, c;
        for (int i = 0; i < e; i++) {
            scanf("%d %d %d", &a, &b, &c);
            dist[a][b] = c;
            dist[b][a] = c; // 无向图
        }

        floydWarshall();

        int minDist = INF, minCity = 0;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = 0; j < n; j++) {
                sum += dist[i][j];
            }
            if (sum < minDist) {
                minDist = sum;
                minCity = i;
            }
        }
        printf("%d\n", minCity);
    }
    return 0;
}

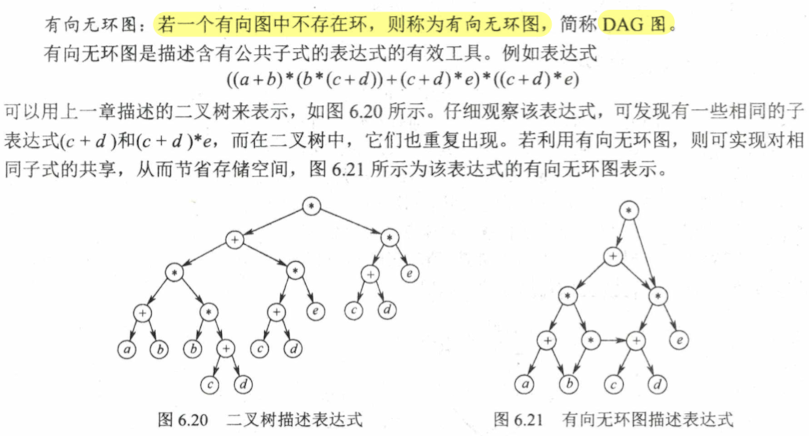
6.4.3 有向无环图描述表达式

image-20240106191530078

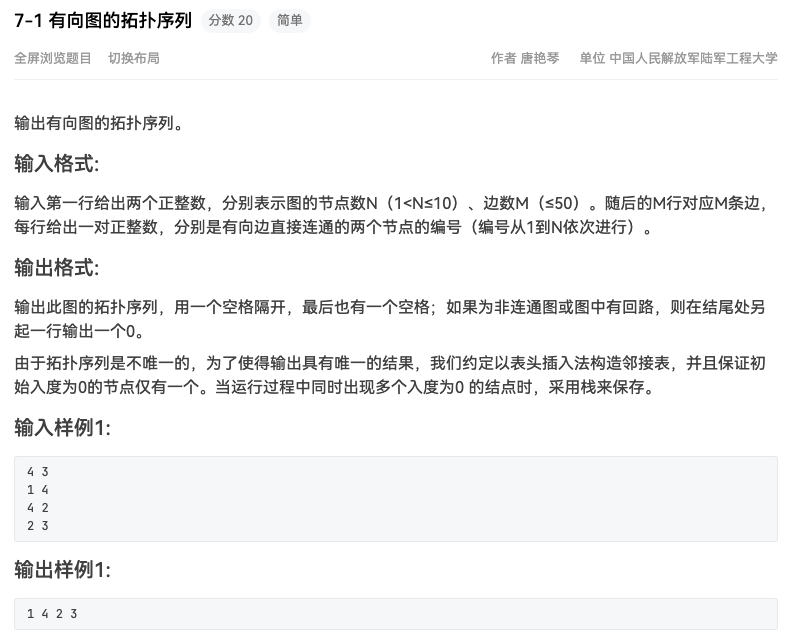
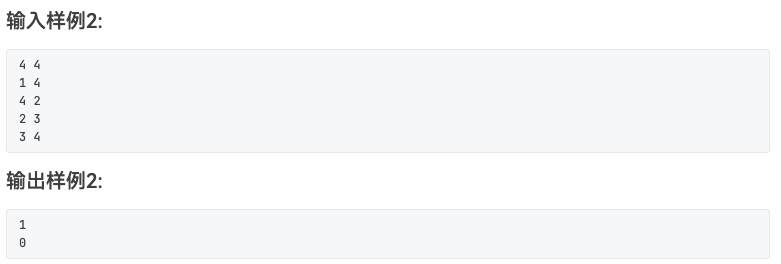
6.4.4 拓扑排序

可能要求代码实现

image-20240108165217583

image-20240106191816166

image-20240106191824406

image-20240106191906324

题目

image-20240108130627123

image-20240108130634920

image-20240108130706640

#include <stdio.h>
#include <stdlib.h>

#define MAXN 10
#define MAXM 50

// 邻接表节点
typedef struct Node {
    int vertex; // 节点编号
    struct Node* next; // 下一个邻接节点
} Node;

// 入度数组
int inDegree[MAXN];
// 邻接表
Node* graph[MAXN];
// 结果数组
int topoOrder[MAXN];
// 栈
int stack[MAXN];
// 栈顶
int top = -1;

// 添加边
void addEdge(int start, int end) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->vertex = end;
    newNode->next = graph[start];
    graph[start] = newNode;
    inDegree[end]++;
}

// 拓扑排序
int topologicalSort(int n) {
    int count = 0; // 计数，记录加入到拓扑序列的节点数
    for (int i = 1; i <= n; i++) {
        if (inDegree[i] == 0) {
            stack[++top] = i; // 入度为0的节点入栈
        }
    }

    while (top != -1) {
        int current = stack[top--]; // 出栈
        topoOrder[count++] = current; // 加入拓扑序列

        Node* temp = graph[current];
        while (temp) {
            int adjVertex = temp->vertex;
            inDegree[adjVertex]--;
            if (inDegree[adjVertex] == 0) {
                stack[++top] = adjVertex;
            }
            temp = temp->next;
        }
    }

    if (count != n) { // 如果节点数不等于n，说明有环
        return 0;
    }
    return 1;
}

int main() {
    int n, m, u, v;
    scanf("%d %d", &n, &m);
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &u, &v);
        addEdge(u, v);
    }

    if (topologicalSort(n)) {
        for (int i = 0; i < n; i++) {
            printf("%d ", topoOrder[i]);
        }
        printf("\n");
    } else {
        printf("0\n");
    }
    return 0;
}

第 7 章 查找

7.1 概念

image-20240106203031831

7.2 顺序查找和二分查找

7.2.1 顺序查找

线性表的顺序查找

要求掌握带哨兵的代码实现。哨兵为a[0]，从后往前找，就不用判断数组是否越界

image-20240106203702223

image-20240106203714055

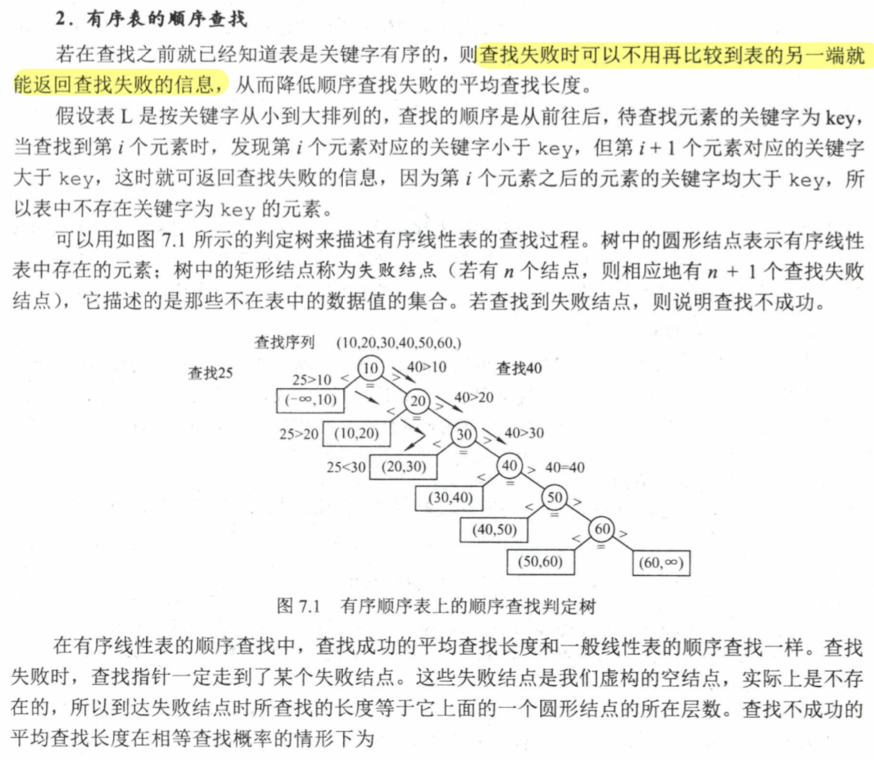
有序表的顺序查找

image-20240106203957878

image-20240106204005757

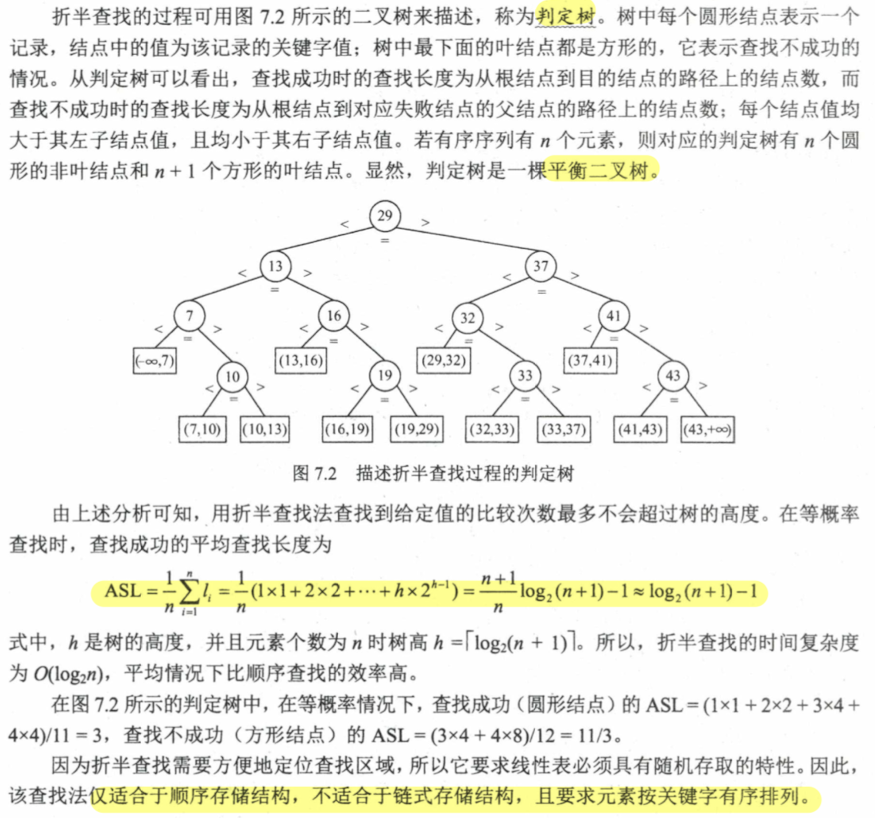
7.2.2 二分查找

image-20240106204356103

int binarySearch(int a[], int val){
    int left = 0, right = n - 1, mid;
    while(left <= right){
        mid = (left + right) / 2;
        if(a[mid] == val) return mid;
        else if(a[mid] > val) right = mid - 1;
        else left = mid + 1;
    }
    return -1;
}

image-20240106205121040

7.2.3 分块查找*

image-20240106205303723

image-20240106205309480

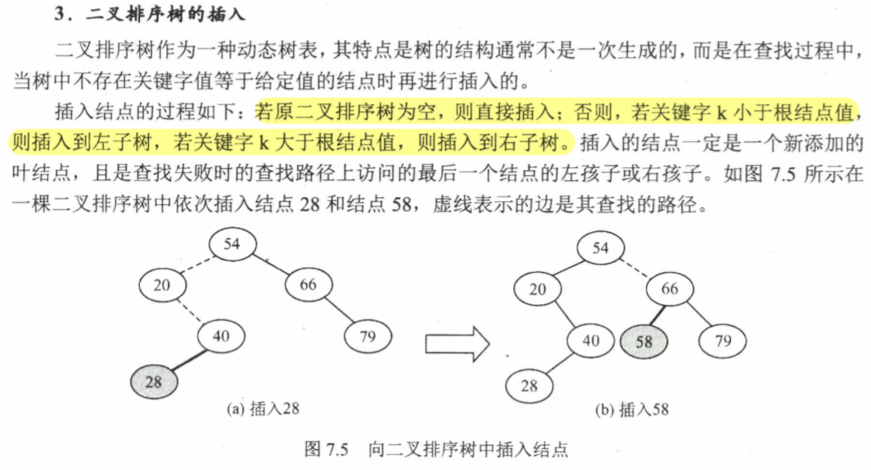
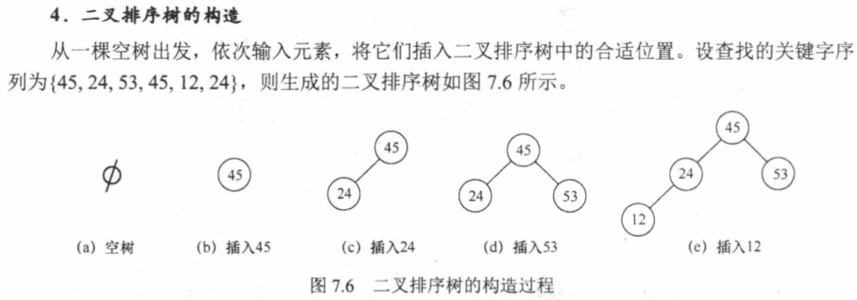
7.3 树形查找

7.3.1 二叉排序树 BST

不要求代码实现

image-20240106205614828

image-20240106205641795

image-20240106205654796

image-20240106205739284

image-20240106205748078

image-20240106210022854

image-20240106210104957

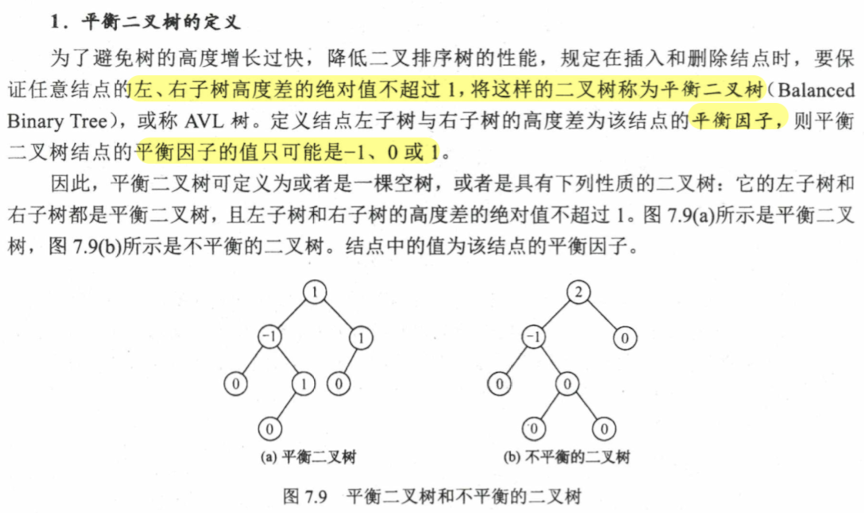
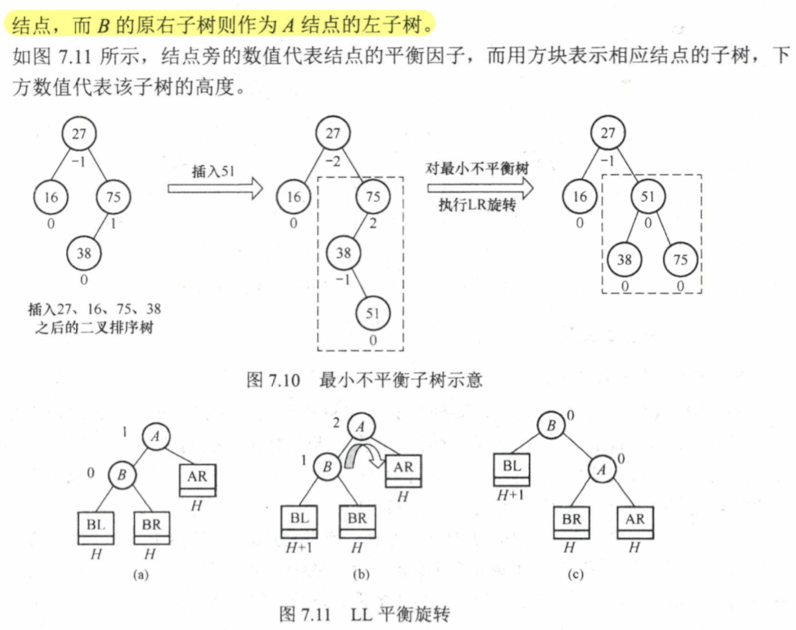
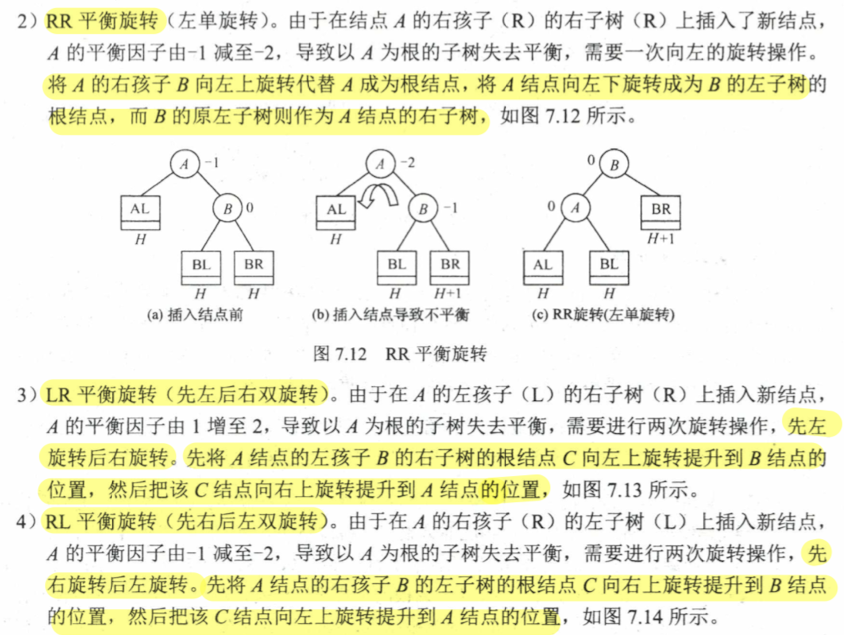
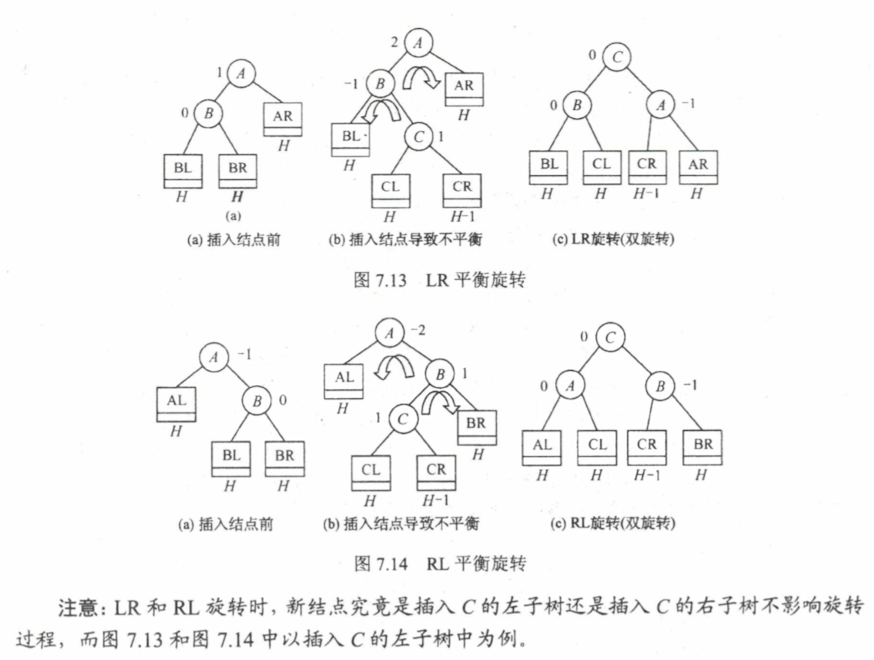
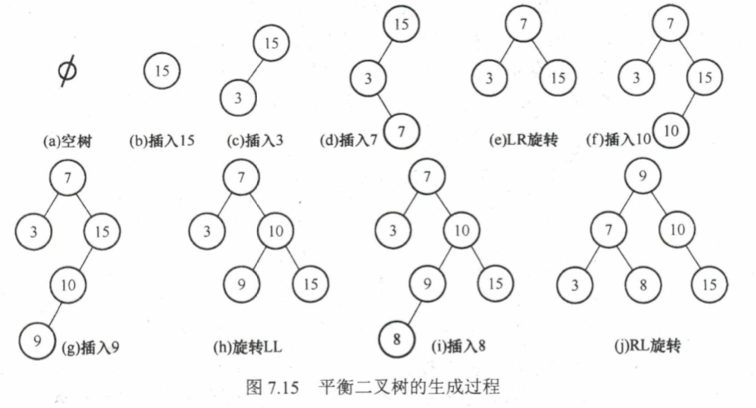
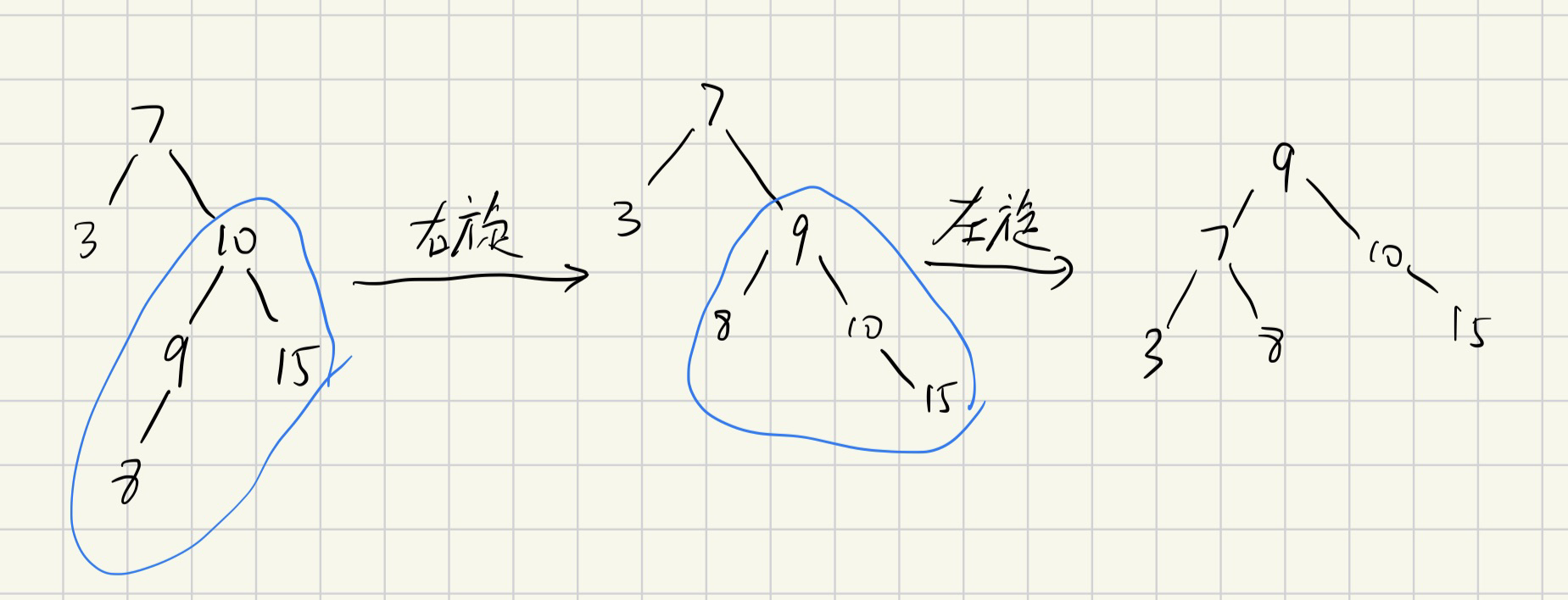
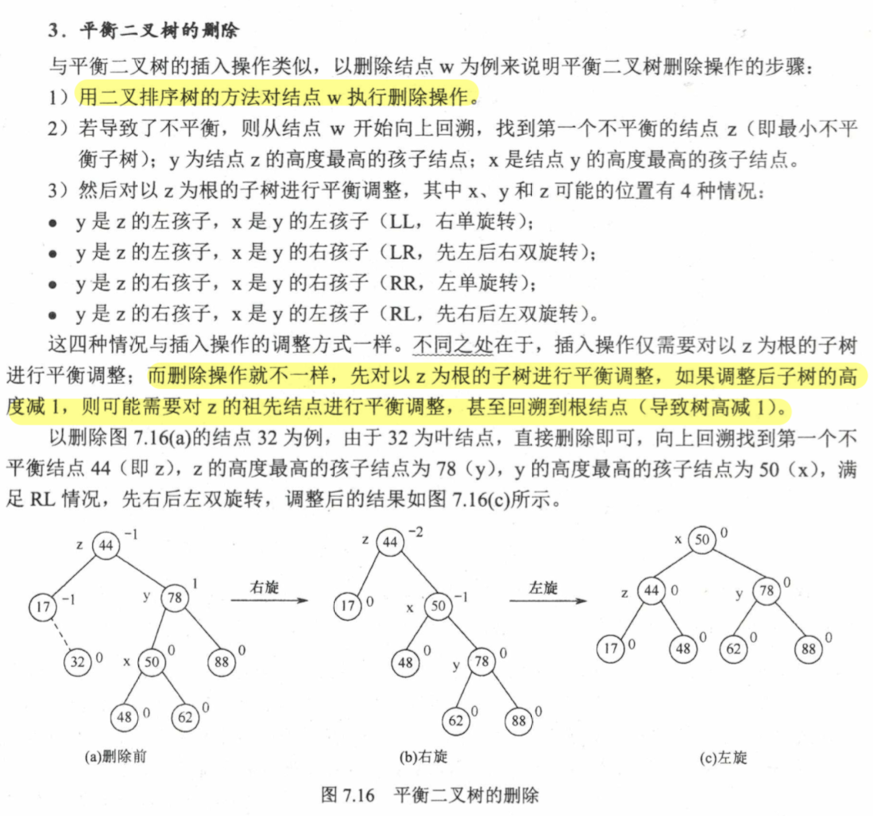
7.3.2 平衡二叉树 AVL

image-20240106210227611

image-20240106212138778

image-20240106212146442

image-20240106212153557

image-20240106212207978

image-20240106212238103

image-20240106212957511

image-20240106213123083

image-20240106213151385

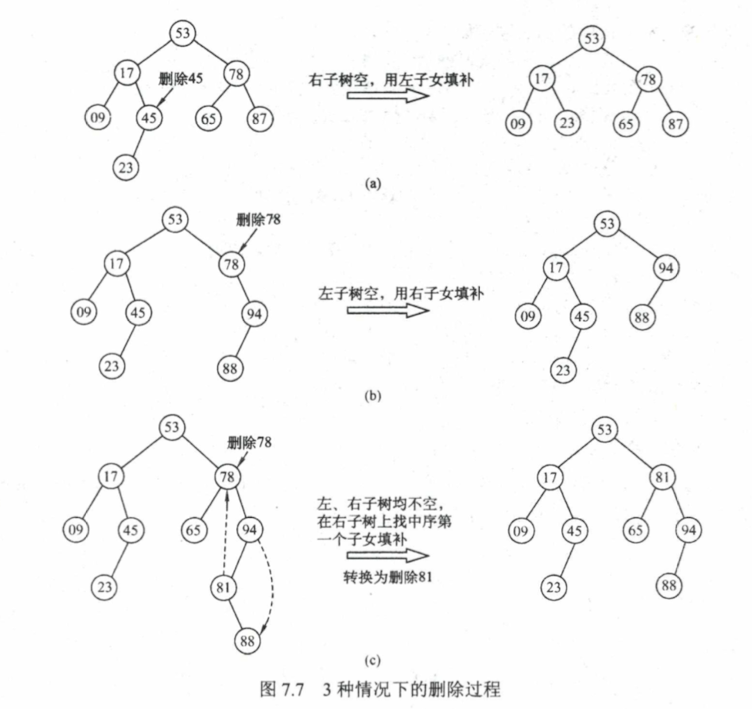
题目

删除根节点时，倾向于把前驱拿上来

image-20240107094441347

7.5 哈希表

7.5.1 概念

image-20240106213435039

7.5.2 哈希函数

image-20240106213658071

image-20240106213707660

7.5.3 冲突

注意是 mod m, 不是 mod k

image-20240106213959213

image-20240106214010196

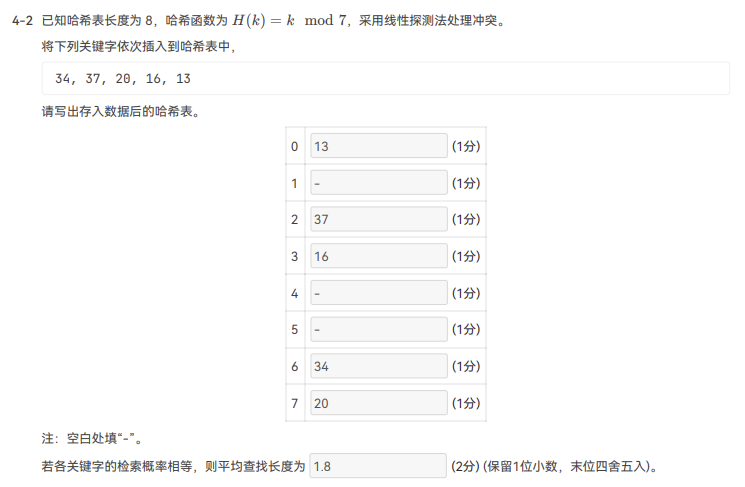
7.5.4 哈希查找和性能分析

要求会构造哈希表，计算成功和失败查找的平均查找长度

image-20240106214521881

image-20240106214528738

题目

image-20240111132601937

image-20240111132613907

第 8 章 排序

8.1 概念

image-20240106214711325

8.2 插入排序

8.2.1 直接插入

要求代码实现

image-20240106214930713

image-20240106214947365

void InsertSort(int a[], int n){
    int i, j;
    for(i = 2; i <= n; i++){
        if(a[i] < a[i - 1]){
            a[0] = a[i]; //哨兵
            for(j = i - 1; a[0] < a[j]; j--)
                a[j + 1] = a[j];
            a[j + 1] = a[0]
        }
    }
}

image-20240106215732517

image-20240106215743118

8.2.2 二分插入

要求代码实现

image-20240106220906225

void InsertSort(int a[], int n){
    int i, j, l, r, mid;
    for(i = 2; i <= n; i++){
        a[0] = a[i];
        l = 1, r = i - 1;
        while(l <= r){
            mid = (l + r) / 2;
            if(a[mid] > a[0]) r = mid - 1;
            else l = mid + 1;
        }
        for(j = i - 1; j >= r + 1; j--)
            a[j + 1] = a[j];
        a[j + 1] = a[0];
    }
}

image-20240106221312966

8.3 交换排序

8.3.1 冒泡排序

image-20240106221626808

image-20240106221649125

image-20240106221846672

8.3.2 快速排序

要求代码实现

image-20240106222010858

image-20240106222149445

void qsort(int a[], int l, int r){
    if(l < r){
        int pivot = partition(a, l, r);// 划分
        qsort(a, l, pivot - 1);
        qsort(a, pivot + 1, r);
    }
}
int partition(int a[], int l, int r){
    int pivot = a[l];
    while(l < r){
        while(l < r && a[r] >= pivot) r--;
        a[l] = a[r];
        while(l < r && a[l] <= pivot) l++;
        a[r] = a[l];
    }
    a[l] = pivot;
    return l;
}

image-20240106222859131