线性代数 学习笔记

注意事项

注意事项

遇到选择题的抽象矩阵，可特殊值法

在大题中遇到奇怪的矩阵方程时，可考虑将矩阵拆为列向量，解多个方程组

上/下三角阵可用于构造行列式

大题求矩阵特征值时，可找相似，但特征向量不同

遇到E，可将其拆为A*A逆

在判线性无关时，不要忘记0向量的特殊情况；0向量和任何向量线性相关。可使用定义法：k1*α1 + k2*α2 = 0, k1 k2 不全为0

具体向量判线性相关时，可求行列式，而不是初等变换

遇到抽象矩阵（矩阵用抽象向量表达）求特征值，可根据定义Aξ＝λξ，用已知向量作为ξ尝试

若矩阵的行和均为a，则 λ = a

出现矩阵与E的组合时，想到特征多项式

二次型是一个数，二次型的转置还是它本身

二级结论

R1矩阵的特征值：迹，0，0

AB和BA有相同的非零特征值；若AB有零特征值，则无法确定BA是否有零特征值；注意AB和BA的阶数可能不同，若小阶矩阵n没有零特征值，则大阶矩阵m有对应相同的特征值和m-n个零特征值

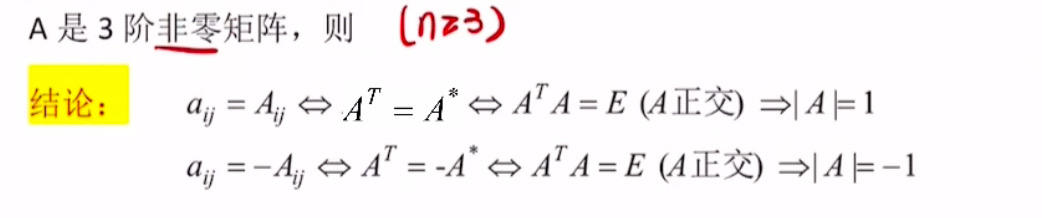
行列式

行列式性质

|AB|＝|A| |B|

余子式M 代数余子式A 行列式展开定理

主子式

范德蒙德行列式

矩阵

伴随矩阵

可逆矩阵

可逆矩阵的证明，可用反证法

若A不可逆，则行列式=0，不满秩，有向量线性相关

性质

初等矩阵 初等变换

初等矩阵：单位矩阵进行1次初等变换

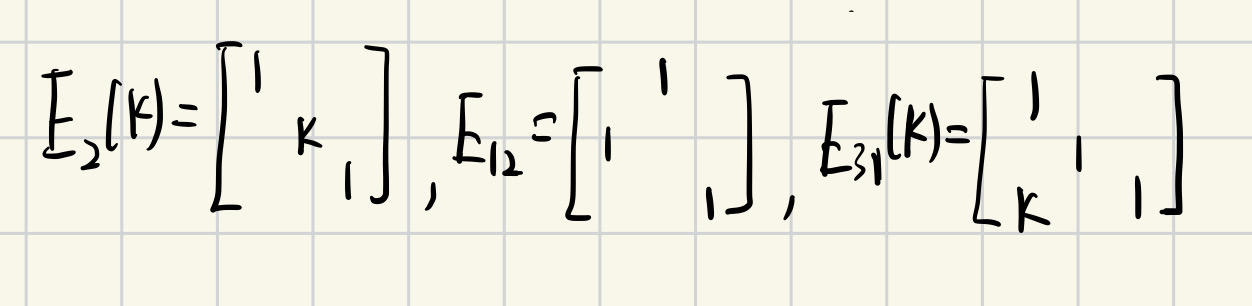
在对负数减负数时特别容易出错

对A进行初等行变换，等价于A左乘对应初等矩阵

秩

若B可逆，则r(AB) = r(A)

若r(AB) < r(A)，则B不可逆

向量组

内积 正交 正交基 正交矩阵

正交矩阵每行/列的模长=1

向量两两正交是性质，不是充分条件（图片中写错了）

等价向量组 同解方程组

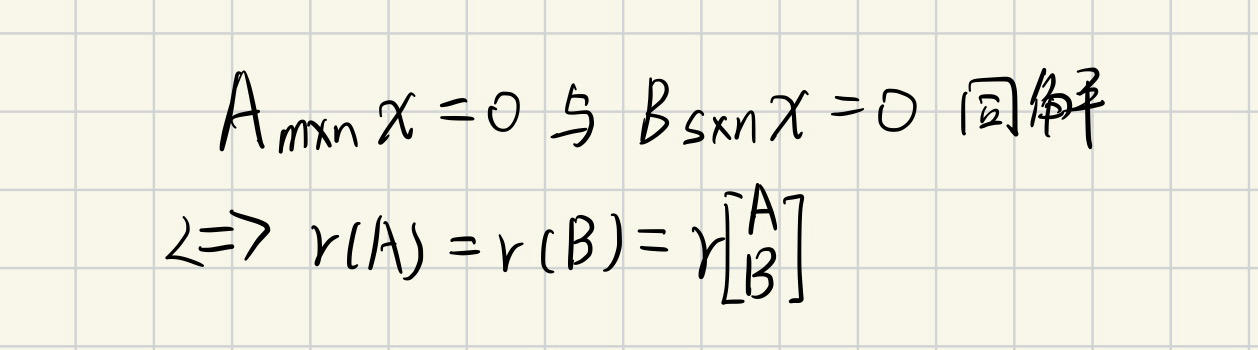
向量空间 基 坐标

过渡矩阵

C为旧基到新基的过渡矩阵

线性方程组

齐次线性方程组

非齐次线性方程组

算非齐次的唯一解时，要化成行最简阶梯形，即使有分式

全解的差是齐次解

齐次解加全解还是全解

基础解系 通解

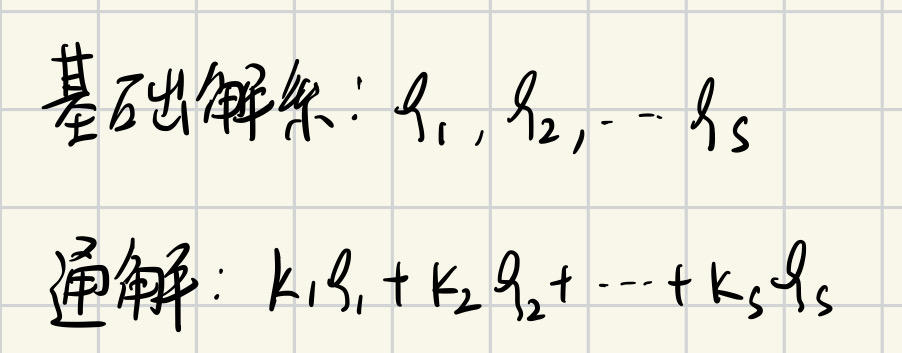
特征值和特征向量

特征多项式

特征值和特征向量

相似对角化的条件

必要条件（性质）：r(A) = n - 零特征值的个数

两矩阵相似

条件：特征值对应相同，且都可对角化

性质：

r(入E-A) = r(入E-B)

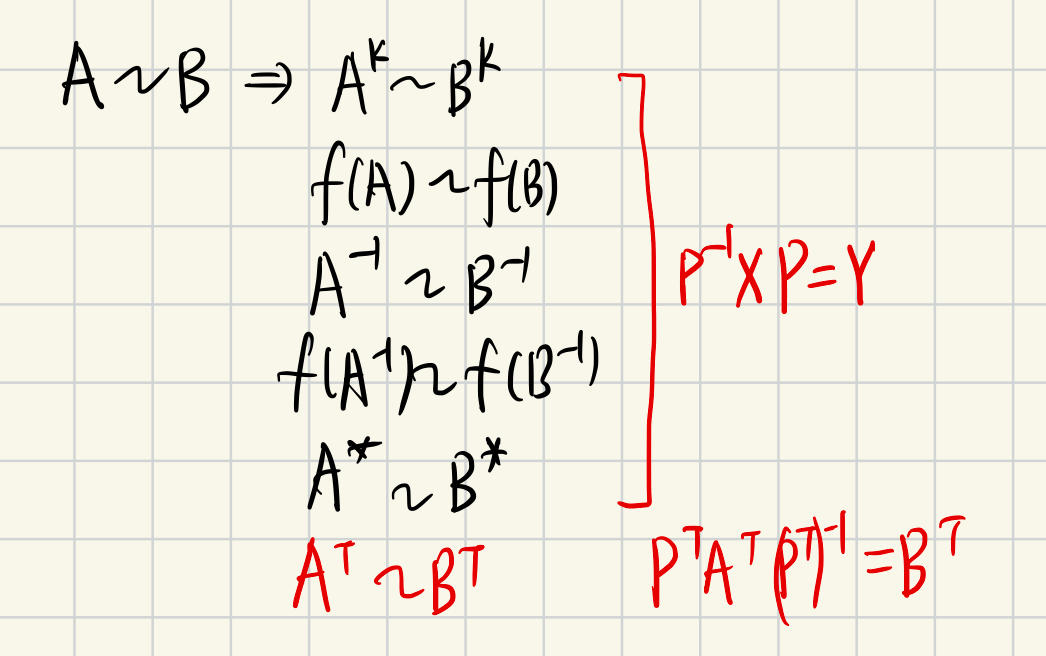
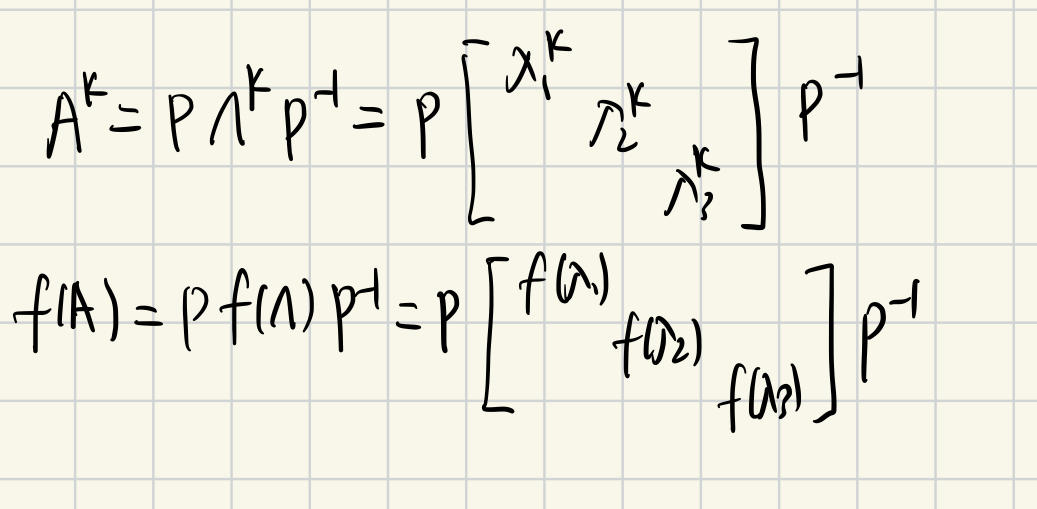
对称矩阵

对称矩阵的属于不同特征值的特征向量相互正交

施密特正交化

正交化只需要对属于相同特征值的特征向量进行，因为属于不同特征值的特征向量已经正交了

二次型

标准形 规范形

配方法化标准形或规范形

配方步骤：先对x1方和所有含x1的项配完全平方

若出现只有2项的情况，第3项系数为0，但在写线性变换方程时要写y3=x3

可逆矩阵C是反解出x后y的系数矩阵

线性变换写作 x=Cy， 其中 C^T A C = 对角阵

正交变换化标准形

正交法不能化为规范形

正交法可以不化标准形，但是变换后的矩阵仍然与原矩阵相似

正交变换满足相似对角化的性质，例如A正交变换得到B，对A和B分别正交法化标准形，得到A到B的变换矩阵

线性变换 合同

两二次型（对称阵）合同的充要条件：

相同的正负惯性指数（规范形相同）

或 相同秩 和 正/负 惯性指数

或 相同 正负 特征值个数

惯性定理

可逆线性变换化为标准形或规范形时，正项个数p与负项个数q不变，r=p+q<=n

因此可以用正交变换法求出特征值后直接得出【规范形】（无需求特征向量）

正定二次型

定义：f(x1,x2,x3) > 0 恒成立 （x不全为0）

充要条件：

正惯性指数 = n（特征值都大于0）

合同于单位阵

顺序主子式都大于0

A正定 等价于 存在可逆P，使A=P^T * P

性质：

主对角线元素都大于0

行列式大于0